Bibliografia complementar:

1. Anton, H. e Rorres, C. - Algebra Linear com Aplicacoes, Bookman, Porto Alegre, 2001Capitulo 11.
2. MIT

1. Tema1-Erros-

   Porque estudar erros

   Calculando erros

   Tipos de erros

   Mudando de base

   Operacoes em binarios

   Representando numeros de ponto flutuante

   
   
2. Tema2-Zeros de Funcoes-

   Motivacao e Introducao

   Metodo da Bisseccao

   Metodo da Falsa Posicao

   Metodo de Iteracao de Linear

   Metodo de Newton-Raphson

   Metodo da Secante

   Isolando Raizes e Criterios de Parada

   Comentarios Finais

   
   
3. Tema3-Sistema de Equacoes Lineares (SEL)-

   Introducao e Sistemas Especiais

   Metodo de Gauss (Parte 1)

   Metodo de Gauss (Parte 2)

   Metodo de Gauss (Parte 3)

   Fatoracao LU

   Metodos Interativos

   Metodo de Jacobi

   Metodo de Gauss - Seidel

   Comentarios Finais

   
   
4. Tema4-Sistema de Equacoes Nao Lineares (SENL)-

   Metodo de Newton-Raphson

   Metodo de Newton-Raphson Modificado

   
   
5. Tema5-Interpolacao Polinomial (Inter)-
   Videos escolhidos pela turma de 2021-2 e sugeridos como Trabalho 5 de 2021/1)
   
   

   Polinomio de Lagrange em C - Mouzinho Raimundo - https://www.youtube.com/watch?v=IsF22ZbzpPo

   Toda a Matematica Gustavo Viegas https://www.youtube.com/watch?v=9LJOlkyedik

   https://www.youtube.com/watch?v=Y9sa2S-ljX8 - Prof. Izaias Neri

   Universidade de Alberta - Canada : https://www.youtube.com/watch?v=3ZwX600OYDE&ab_channel=LindseyWestover - uma aula bem completa -

   https://engcourses-uofa.ca/books/numericalanalysis/polynomial-interpolation/lagrange-interpolating-polynomials/ - esse bem longo

   https://engcourses-uofa.ca/books/numericalanalysis/polynomial-interpolation/lagrange-interpolating-polynomials/ -

   https://www.youtube.com/watch?v=dTGqOj1NZwY em python

   Video com equacoes : https://youtu.be/ZFCDp3oXPII

   Exemplo pratico: https://youtu.be/HXoQRKLMwaI - exemplo numerico

   Implementacao: https://youtu.be/Ty_kV-N7qB4 - programa em Python

   https://www.youtube.com/watch?v=vAgKE5wvR4Y - ENME 03 UMBC Numerial Methods

   https://www.youtube.com/watch?v=GtJKUIG9KXI - Oscar Veliz

   https://www.youtube.com/watch?v=haKcN0HmXQI fala genericamente e rapido

   https://www.youtube.com/watch?v=ppBsL54_OO0 - matematica universsitario - video longo

   https://www.youtube.com/watch?v=ppBsL54_OO0 - Canal ensino e inform. - exemplos - prof. Altamir Araldi

   links: https://www.youtube.com/watch?v=B2wqZKZv3O0

   https://www.youtube.com/watch?v=khZv01Om6is&t=292s - Mix de Math the beautiful :

   Explica da utilizacao : https://www.youtube.com/watch?v=7yecmvEcGJM (6:11)

   Implementacao : https://www.youtube.com/watch?v=nHlAx4vIf-g

   https://classroom.google.com/c/NDE2Mjg5MTcxNDk0/a/NDM3NDkxNzQyNDE3/submissions/by-status/and-sort-first-name/student/MTI4MTM1MzcwNTk4

   https://www.youtube.com/watch?v=haKcN0HmXQI

   https://www.youtube.com/watch?v=deoHewS3AmA

   https://www.youtube.com/watch?v=9LJOlkyedik - Introd. Interpolacao Polinomial

   Aula 22 Metodos: Interp. de Lagrange - Codigo em Python para Interp. Lagrange: https://www.youtube.com/watch?v=pjxhqeeeIqw

   Codigo de Lagrange (Python) - https://www.youtube.com/watch?v=tf2zKz8FVzU

   univesp - Leonidas Brandao - https://www.youtube.com/watch?v=OJnHtKFjZcw

   Milena Brandao - aula 12 - 3 videos: https://www.youtube.com/watch?v=5m7Mm-kyWkg

   Alunos de Um curso de Eng Civil - https://www.youtube.com/watch?v=LTafC2x-FUQ

   https://www.youtube.com/watch?v=DZdSEz8lhPg

   Manu Santos - UFC : https://www.youtube.com/watch?v=ppBsL54_OO0
   https://www.youtube.com/watch?v=pjxhqeeeIqw

   https://www.youtube.com/watch?v=SrWq4tAhws4&t=1070s&ab_channel=ProfessorMauricioMancini

   https://www.youtube.com/watch?v=8Ez6yOPA3L0&ab_channel=OnezimoCardoso

   https://www.youtube.com/watch?v=JZoKXDb55fw - UFMG - Fabricio Murai

   6. Tema6-Integracao Numerica (IN)-

      Introducao e Motivacao

      Metodo dos Trapezios

      Metodo dos Trapezios (Erros)

      Metodo de Simpson

      Metodo de Simpson (Erros)

      Quadratura Gaussiana e Comparacao dos Metodos

   
   
   7. Tema7-Equacoes Diferenciais Ordinarias (EDO)-

      Introducao e Motivacao

      Introducao e Motivacao (continuacao)

      Metodo de Euler

      Metodo de Euler: convergencia

      Metodo baseados na serie de Taylor

      Metodo de Runge-Kutta e mais

      Sistemas de EDO: Metodo de Euler

      Sistemas de EDO: Metodo de Runge-Kutta

      Sistemas de EDO de ordem mais alta

   
   
   8. Tema8-Ajuste de Curvas (AC)-:
      Ajuste de Curvas por Minimos Quadrados (MQ)-
      
      • Aula 30 - Jalberth Fernandes- https://www.youtube.com/watch?v=ppwU4LaWmto& list=PLIHE326iMCHAKqaupMhTorHU4vd5rmrmi&ind ex=30
      • Aula Curso UFRGS - https://pt.m.wikipedia.org/wiki/M%C3%A9todo_dos_m%C3%ADnimos_quadrados
        https://www.youtube.com/watch?v=KzbokLSpILY
        https://www.ufrgs.br/reamat/AlgebraLinear/livro/s14- mx00e9todo_dos_mx00ednimos_quadrados.html
        https://site.tc.com.br/blog/educacao-financeira/financas-programacao/metodo-dos- minimos-quadrados-ordinarios
        http://astro.if.ufrgs.br/minq/
      • Aulas - Murakami - Matematica Rapidola
      • Aula - Thaty Sakate - canal MathemaThike - https://www.youtube.com/watch?v=oxql93ShyLs
      • Engenheiro de Plantao
      • Aula 10 - Univesp - Joyce Bevilacqua - https://www.youtube.com/watch?v=zIlOwe-qfKM
      • Aula 11 - Univesp - Joyce Bevilacqua - https://www.youtube.com/watch?v=kaL-j412a5A
      • https://www.youtube.com/watch?v=Q6W-LizzfwY&t=0s
      • http://www.decom.ufop.br/prof/marcone/Disciplinas/MetodosNumericoseEstatisticos/ QuadradosMinimos.pdf
      • https://www.youtube.com/watch?v=oxql93ShyLs
      • https://www.ufrgs.br/reamat/AlgebraLinear/livro/s14-mx00e9todo_dos_mx00ednimos _quadrados.html
      • https://pt.wikipedia.org/wiki/M%C3%A9todo_dos_m%C3%ADnimos_quadrados#:~:t ext=O%20M%C3%A9todo%20dos%20M%C3%ADnimos%20Quadrados,estimado% 20e%20os%20dados%20observados
      • Aplicacoes da Algebra Linear. Matematica. Disponivel em:. INSTITUTO DE FISICA, Apostila de Fisica Experimental III, Universidade Federal Fluminense, Niteroi (2015).
      • SIQUEIRA, B. Introducao ao Calculo Numerico - Metodo dos Minimos Quadrados.: .
      • Video:https://www.youtube.com/watch?v=fM7551BIB0Y
      • https://www.ime.unicamp.br/~valle/Teaching/2015/MS211/Aula17.pdf
      • http://wwwp.fc.unesp.br/~adriana/Numerico/Ajuste.pdf
      • https://www.ufrgs.br/reamat/CalculoNumerico/livro-sci/adc.html
      • https://www.youtube.com/watch?v=mRJ7uqaCeb0
      • link video : https://www.youtube.com/watch?v=oxql93ShyLsM/li>
      • Implementacao em Python https://colab.research.google.com/drive/1gpIfwFBzsiSPe8IyXKO7W7yzN1OucFi0?usp=sharing
   
   
   

   ---

Trabalhos 2024 / 2

Trabalhos 2024 / 1

1. TRABALHO 5 - 2024 /1 - Area sob polinomios:
   

   Depois de ler sobre o assunto na bibliografia disponibilizada (e pela internet em videos e aulas que vc encontrar), voce vai pegar seu numero de matricula e gerar com ele um polinomio , p(x), de grau 8.
   Em p(x) o algarismo mais a esquerda da sua matricula sera a constante para o x⁸, e assim sucessivamente ate que a constante indepedente do polinomio seja o algarismo mais a direita de sua matricula.
   Com esse polinomio considere uma curva y=p(x) com x de 0 e 10.
   Usando as regras de integracao numerica calcule a area interior a esse polinomio, o eixo dos x, e as retas x=0 e x=10 com erro menor que 0,000000001.
   Em outras palavras, use esse polinomio e as formulas de erro maximo para saber que distancia h voce precisa considerar entre cada x_i.
   O numero de pontos entre 0 e 10 tem que no minimo ser 100.
   Considerando esses aspectos, gere uma lista de pontos ( x_i ; y_i=p(x_i)) e integre essa lista numericamente por pelo menos 2 metodos numericos (i. e. use metodos de integracao numerica de Newtons-Cotes) .
   Usando as regras de integracao de polinomio de Calculo diga qual a area real desta regiao.
   Compare se os erros reais (que voce obteve) com os previstos pelas formulas.
   Apresente seu polinomio, seus pontos, os erros (reais e preditos) e as areas obtidas em sala de aula.

   Esse trabalho tem a nota final composta por 2 entregas a serem postadas no Classroom:
   1- A solucao feita por voce dos elementos do trabalho apresentados digitalmente (ou fotografados) e incluida no Classroom; e
   2- A foto de voce em sala de aula mostrando seu polinomio, explicando como obteve a lista de pontos, e a comparacao dos erros. Inclua essa foto tambem na sua area no Classroom.
   Entrega do item 1: - 19/06/2024.
   Entrega do item 2: - 26/06/2024.

---

2. TRABALHO 4 - 2024 /1 - Sistemas nao lineares ou zeros de funcoes vetoriais:
   

   Depois de ler sobre o assunto na bibliografia disponibilizada, voce vai propor um sistema de pelo menos 2 equacoes e 2 incognitas e resolve-lo. Pelo menos uma destas equacoes deve ser uma parabola e um circulo. Desenhe graficos destas equacoes no plano real e as manipule de forma que tenham pelo menos 2 pontos de encontro ( cruzamentos ou intersecoes ) . Esses pontos em que voce ve que as equacoes se cruzam serao as aproximacoes iniciais do metodos iterativo que voce escolhera para resolver o sistema nao linear. Depois de resolver o sistema voce deve prepara uma apresentacao do mesmo para mostrar a turma em sala de aula.

   IMPORTANTE: Combine com os colegas de modo a que cada um tenha um sistema diferente de todos os demais.
   Esse trabalho tem a nota final composta por 2 entregas a serem postadas no Classroom:
   1- A solucao feita por voce do sistema que escolheu apresentada digitalmente (ou fotografada) e incluida no Classroom; e
   2- A foto de voce explicando essa solucao em sala de aula incluida tambem na sua area no Classroom.
   Entrega Parte 1 - 29/05/2024 .

---

3. TRABALHO 3 - 2024 /1 - Tema 3 - Sistemas de Equacoes Lineares:
   
   Considerando a aula de 24/04/2024 descreva:
   1- Simples e diretamente (com suas palavras) como se resolve um sistema pelo Metodo de Gauss-Jacobi e pelo Metodo de Gauss Seidel;
   2- Considerando uma certa ordem de linhas e colunas como pode-se dizer que ele converge por esses metodos;
   3- Como se usa o criterio de Sassenfeld para verificar a convergencia de um sistema;
   4- Seria possivel tornar o sistema
   
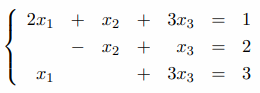
   convergente por algum dos metodos iterativos?
   5- Resolva o sistema acima com tolerancia < 0,1 e com um chute inicial diferente de ( 0, 0, 0).
   
   IMPORTANTE: Nada de 2 chutes iniciais iguais na turma !.
   Entreguem as respostas no Classroom fotografadas e, na forma fisica, no papel que iniciaram em sala, na segunda feira 29/04/2024.
   Voce poderia sugerir uma regra para facilitar a convergencia de um SISTEMA Linear ? ?
   Entrega no Classroom - 29/04/2024.

---



4. TRABALHO 2 - 2024 /1 - Tema 2 - Zeros de Funcoes:
   
   Objetivo: Encontrar raizes de um polinomio por 2 metodos de quebra .
   Enunciado: Resolva pelos metodos de bissecao e falsa posicao os ZEROS de um polinomio de grau maior ou igual a 3 que tenha raizes reais.
   2 .1 - Utilize tabelas e explique de forma organizada cada iteracao que voce fez.
   2 .2 - Compare depois as duas solucoes, dizendo se convergiram, para as mesmas raizes com que tolerancia e com quantas iteracoes.
   2 .3 - Escreva duas receitas, passo a passo, que explique como resolver o problema de encontrar as raizes de polinomios em um dado intervalo e tolerancia por esses metodos.
   2 .4 - Responda: o que significa ordem de convergencia de um metodo computacional ?
   Nao pode haver 2 polinomios iguais na turma!

   
   Entrega no Classroom - 17/04/2024.

---



5. TRABALHO 1 - 2024 /1 - Tema 1 - Erros e Ponto Flutuante:
   
   Assista os videos do TEMA 1. Leia os capitulos corresponentes na bibliografia disponibilizada. Procure mais material sobre representacao de numeros de ponto fixo e operacoes de numeros de ponto flutuante pela WWW. Depois responda as perguntas perguntas abaixo com suas palavras. E prepare um explicacao rapida para apresentar em sala de aula aos demais com 5 sub-itens. Ambos serao usados na sua nota deste tema e devem ser incluidos no classroom.
   
   O texto (item 1) deve ser com suas palavras respondendo:
   1.1- Se for desconhecido o valor exato de algo como se avalia os erros absolutos e relativos?
   1.2- Defina Float ou ponto flutuante. Como se fazem operacoes de aritmetica (soma, subtracao, multiplicacao) com eles?
   Entregue o material do item 1 no classroom.

   
   A explicacao (item 2) deve ser direta e ter um material auxiliar (preparado por voce para levar 10 minutos) em uma apresentacao em sala de aula. Essa deve conter os 5 seguintes sub-itens:
   2.1 - Como se converte um numero decimal para a binario.
   2.2 - Como se trabalha com um numero que tiver uma parte fracionaria (algo menor que 1, por exemplo).
   2.3 - Descreva a representacao de ponto flutuante (float) e qual a importancia da mantissa, base, expoente e numero de digitos.
   2.4 - Apresente pelo menos um exemplo com 4 numeros somados que leve a erros e quebra de propriedades da soma (como por exemplo associatividade, comutatividade, etc. )
   2.5 - Apresente um exercicio aos colegas sobre o item anterior e o resolva.
   Entregue o material do item 2 em pdf no classroom.

   
   Entrega no Classroom - 01/04/2024.


Qualquer revisao em sala - 17/04/2024.

---


Trabalhos dos diversos anos:
[Inicio][Ementa][Links][Bibliografia]

Trabalhos 2023 / 2

1. TRABALHO 1 - 2023 /2 - Representacao de Ponto Flutuante e Erros:
   
   Assista os videos do TEMA 1. Leia os capitulos corresponentes na bibliografia disponibilizada. Procure mais material sobre representacao de numeros de ponto fixo e operacoes de numeros de ponto flutuante. Depois responda as perguntas que seguem . Que servirao de base para uma avaliacao presencial em sala de aula.
   Entrega no Classroom - 4/09/2023.



---



2. TRABALHO 2 - 2023 /2 - Zeros de Funcoes:
   Utilizando o tabelamento, ou seja colocando em tabelas cada passo (iteracao) que voce fizer, resolva pelos metodos de quebra (bissecao e falsa posicao) a solucao da equacao:
   x²+ln x
   no intervalo [0.5 ; 1] , com uma tolerancia menor que 0.05 , isto e' : || F(x) ||<0.05. Depois compare as duas solucoes, dizendo se convergiram nas mesmas iteracoes e para as mesmas raizes.
   Finalmente escreva duas receitas, passo a passo, que expliquem a um robot como resolver o problema de encontrar as raizes por esses metodos, de uma funcao generica em um dado intervalo e tolerancia.
   Nao deixe de ler e assisti os videos de todo esse tema, para se preparar para uma avaliacao presencial em sala de aula, no assunto.
   Entrega no Classroom - 11/09/2023 (Estudo Dirigido em sala no mesmo dia.)



---




3. TRABALHO Extra - 2023 /2 - Implementacao do Metodo de Newton - Raphson:
   Esse trabalho pode ser em qualquer linguagem e mesmo com qualquer utilitario que voce domine (como Mathlab, R, Excell, etc.).
   A entrega deve ser na forma de inclusao no classroom de prints da tela com o resultado como uma tabela das diversas iteracoes. A funcao que deve ser usada sera a mesma do trabalho anterior (2- 2023/2) e na forma de fazer um refinamento de alguma raiz inicial. Mas o mais importante: antes de iniciar assita aos videos: Metodo do Ponto Fixo, Metodo de Newton, Metodo da Secante, e a implementacao do Metodo de Newton e do Metodo da Secante ) do curso de Metodos Numericos no YOUTUBE da Dra. Emanuele Santos da UFC. Pois alem dos prints da implementacao voce deve , escrever um paragrafo, a mao, com suas palavras sobre como pode ocorrer do metodo de Newton nao convergir (fotografar e postar no classroom) .
   Entrega no Classroom - 20/09/2023 .



---



4. TRABALHO 3 - 2023 /2 - Implementacao do Metodo de Jacobi:
   Esse trabalho pode ser em qualquer linguagem e mesmo com qualquer utilitario que voce domine (como Mathlab, R, Excell, etc.).
   A entrega deve ser na forma de inclusao no classroom de uma foto com voce mostrando o trabalho na sala de aula e assistido pelos colegas. Sua implementacao deve resolver um sistema de 9 equacoes a 9 incognitas, a ser fornecido pelo usuario. Inicialmente o programa vai verificar a convergencia usando o Criterio das Linhas ou da Diagonal Dominante, avisando se esse nao for atendido e, pedindo para se trocar a ordem das equacoes e fornecer o sistema de novo, neste caso. Depois deve pedir qual erro relativo se admite como convergencia. E usar o calculo da diferenca relativa entre cada iteracao sucessiva ser menor que esse erro ou atingir 2 mil iteracoes como criterio de parada. Esse programa deve ser mostrado para a turma rodando na aula de 27/09/2023; Ou seja, a entrega deve ser durante a aula, na forma de sua apresentacao aos demais da turma. .
   Estudo Dirigido em sala 25/09/2023
   Entrega no Classroom - 27/09/2023 .



---



5. TRABALHO 4 - 2023 /2 - Integracao (penultimo trabalho):
   Leia os capitulos correspondentes a esse TEMA na bibliografia disponibilizada (ou seja nos Topicos 2, 3 e 4 do Texto da UAB; no Cap. 8 do texto de Professores da UFF, e no Cap. 6 do texto do Prof. Marco Antonio).
   Assista os videos das aulas gravadas sobre o tema disponibilizados aqui e no Classroom .
   Ao ler , pesquisar e assitir esse material fique especialmente atendo a:
   • Relacao entre a Soma de Riemann , a regra dos Retangulos e as formas de se integrar numericamente uma lista de dados (nao representados por equacoes) originados de experimentos.
   • Este trabalho consiste de uma implementacao a ser apresentada em sala e entregue como a do TRABALHO 3 - 2023/2 .
   • Ou seja, a entrega deve ser durante a aula de 01/11/2023; na forma de apresentacao da implementacao aos demais da turma e inclusao da foto desta no Classroom .
   • Unico requisito da implementacao: o numero de pontos considerados para fazer a integral ser definido pelo usuario em tempo de execucao.
   • Se espera que o aluno justifique na apresentacao o metodo escolhido para calculo da area abaixo dos pontos considerados (ou integral) .
   Entrega no Classroom - 01/11/2023 .
   Esse tema nao abrange estudos dirigidos ou testes outros.
   As duas partes da nota correspondem a apresentacao em sala e a entrega no Classroom.
   Mas alternativamente , impossibilitado de apresentar em sala no dia o aluno pode gravar a apresentacao e envia-la a professora ate essa data.

   ---

   
   
6. TRABALHO 5 - 2023 /2 - Sistemas nao lineares ou zeros de funcoes vetoriais (ultimo trabalho):
   Depois de assistir os videos do TEMA 4 e ler sobre o assunto na bibliografia disponibilizada, voce vai procurar exemplos diferentes dos que constam dos nossos materiais didaticos (lembre que ha muito material relacionado a nosso curso) . Destes exemplos deve escolher um, de qualquer um dos dois metodos (Newton- Raphson - NR ou NR Modificado) que tenha entendido bem e explicar como se chegou a resposta deste exemplo em sala de aula, nas proximas quartas feiras de novembro, ou se preferir pela internet na proxima segunda feira (12 de novembro). Um ponto importante sera descrever claramente o que se deve fazer para tentar encontrar todas as raizes do exemplo. As explicacoes pela internet devem ser sincronas, no horario de nossas aulas.
   Essa atividade tem a nota final igual a media de 2 entregas a serem postadas no Classroom:
   1- A solucao feita manualmente por voce do exemplo escolhido, fotografada e incluida no Classroom; e
   2- A foto de voce explicando esse exemplo em sala de aula, ou um print da tela de voce dado a mesma explicacao pela internet. Qualquer uma, incluida na sua area no Classroom.
   Entrega Final - 27/11/2023 .



---




---

Trabalhos 2022 / 2

1. TRABALHO 1 - 2022 /2 - Representacao de Ponto Flutuante e Erros:
   
   Assista os videos do TEMA 1. Leia os capitulos corresponentes na bibliografia disponibilizada. Procure mais material sobre representacao de numeros de ponto fixo e operacoes de numeros de ponto flutuante. Prepare um ppt explicando: 1 - como se converte um numero na base 10 para a base binaria se esse numero tiver uma parte fracionaria . 2- O que e a representacao de ponto flutuante e a importancia dos elementos mantissa, base, expoente e numero de digitos. 3- Usando um exemplo com pelo menos 4 numeros somados, explique como mesmo esta operacao basica pode levar a erros e quebra de (propriedades da matematica como) associatividade. Entregue esse material em pdf no classroom, apresente em aula ate a data de entrega. Voce pode tirar qualquer duvida sobre esse tema com a professora , nos horarios de aula ( de acordo com o calendario estabelecido ) ou por e-mail.
   Entrega dos materiais desenvolvidos pelos alunos no Classroom - 31/08/2022 ;
Apresentacao de cada um dos alunos ( aos demais alunos em sala ) em 31/08 a 05/09/2022 ;
Fechamento das Notas deste trabalho : 12/09/2022 ( depois desta data nao sera possivel mais altercoes da nota recebida neste trabalho ) .

---



2. TRABALHO 2 - 2022 /2 - Calculo de Zeros de Funcoes:
   
   Depois de assistir os videos do TEMA 2 ( e ler a bibliografia disponibilizada ) prepare um texto em doc respondendo as perguntas abaixo . Depois organize uma aula em ppt explicando os sequintes aspectos :
   2 . 1 - Como voce pode descobrir se em um dado intervalo existe uma raiz de uma funcao continua? E como voce pode ter uma dica de quantas raizes podem ter em todo o seu intervalo de definicao?
   2 . 2 - Qual a diferenca entre os Metodos da Bissecao e da Falsa Posicao. Mostre essa diferenca entre ambos muito claramente usando graficos aplicados a um exemplo numerico onde voce resolve o calculo da raiz de uma funcao em um intervalo. Nesta solucaoo use uma tolerancia entre o erro relativo menor que 0,1 % .
   2 . 3 - Usando um exemplo explique como se encontram as raizes de uma funcao pelo Metodo de Newton-Raphson (ou das tangentes) . Explique em um texto e na sua aula sobre as condicoes para haver convergencia neste metodo.
   2 . 4 - Procure mais textos e videos sobre outros metodos para o calculo dos Zeros de Funcoes alem dos 3 acima mencionados. Escreva sobre eles no seu texto e depois fale na sua apresentacao sobre as propriedades, vantagens, desvantagens, aplicacoes e limitacoes deste metodos.
   DICA:
   Se quizer voce pode usar programas para ilustrar as respostas e sua apresentacao .
   Entrega no Classroom - 21/09/2022 ;
   Apresentacao de cada um dos alunos ( aos demais alunos em sala ) de 14/09 a 21/09/2022 ;
   Fechamento das Notas deste trabalho : 26/9/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



3. TRABALHO 3 - 2022 /2 - Resolvendo Sistemas de Equacoes Lineares:
   
   Depois de assistir os videos do TEMA 3 ( e ler a bibliografia disponibilizada e em especial a ref. 5 ) a idea deste trabalho e' voce ser o professor, e pode aproveitar para criticar bem sua professora mostrando o que ela faz de errado e precisa melhorar. Mas como temos que tambem seguir no assunto do curso vamos fazer 2 coisas ao mesmo tempo. Aproveitanto para alem de criticar aprender a materia. Assim "prepare uma aula de exercicios para seus alunos" em que voce com apenas 4 exercicios bem escolhidos e preparados explicara' os 4 Principais metodos de Solucao de Sistemas de Equacoes Lineares inclusive mencionando os testes iniciais de verificacao de haver solucao . Depois organize essa aula em ppt e outras midias (quadro negro, video seus ou de outros, programa, planilha com solucao, etc) explicando os sequintes aspectos principais deste tema do curso:
   3 . 1 - O metodo de solucao direta de Gauss e como se usa o pivoteamento nele.
   3 . 2 - O metodo da fatoracao de Cholesky , dizendo em que casos ele seria uma boa escolha.
   3 . 3 - Metodo de Gauss - Jacobi com verificacao de convergencia e possivel alteracoes iniciais do mesmo .
   3 . 4 - Metodo de Gauss - Seidel (usando o mesmo exemplo de 3.3 ) mas com a verificacao de convergencia menos restritiva e mais adequada a esse .
   Deixe disponivel para "seus alunos" o material que voces desenvolveu e usou "em sala" no classroom . Nao deixe de incluir a solucao completa dos exercicios ou seja nao deixe de fazer um gabarito dos exercicios .
   Entrega no Classroom - 05/10/2022 ;
   Apresentacao de cada um dos alunos ( aos demais alunos em sala ) de 28/09/2022 a 5/10/2022;
   Fechamento das Notas deste trabalho : 10/10/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



4. TRABALHO 4 - 2022 /2 - Interacao Numerica:
   
   Leia os capitulos correspondentes a esse TEMA na bibliografia disponibilizada (ou seja na Aula 7 , Topicos 2, 3 e 4 do Texto da UAB; no Cap. 8 do texto de Professores da UFF, e no Cap. 6 do texto do Prof. Marco Antonio). Procure mais sobre Quadratura Gaussiana pela internet e assista os videos das aulas gravadas. Ao ler , pesquisar e assitir esse material fique especialmente atendo a:
   • Relacao entre a Soma de Riemann , a regra dos Retangulos e as formas de se integrar numericamente uma lista de dados originados de experimentos.
   • Definicao de Ordem de uma regra de integracao.
   • Aproximacao do valor da integral analitica que se obtem com as regras de Newton-Cotes;
   • Ideia base da quadratura Gaussiana (nao manter mais os intervalos iguais mas ajustar os intervalos para fazer uma integral exata, tabelar os pontos de avaliacao da funcao entre -1 e 1, e mudar os limites da variavel muda de integracao para se ter resultado exato em outros limites).
   • Entenda que na quadratura Gaussiana e nas regras dos Retangulos, Trapezios e Simpson sao usadas as mesmas letras, simbolos ou variaveis para coisas diferentes.
   Este trabalho consiste de respostas a algumas perguntas e uma implementacao.
   As respondas nao devem ser com textos copiados mas com suas palavras, e sao a essas perguntas:
   1. Como voce faria para melhorar alguma confusao causada pelos metodos que usam os mesmo simbolos (neste tema) para coisas diferentes?
   2. Quando a quadratura Gaussiana nao e' usavel para solucao de um problema de integracao?
   3. Suponha que voce tenha uma lista de pontos f(x) originados de um esperimento, no qual a variavel x_i esteja sempre definida a intervalos iguais das suas vizinhas x_i+1 e x_i-1 . Escolha um dos metodos estudados para implementar o calculo da area entre o eixo dos pontos x_i e os experimentos medidos f(x_i) . Faca um programa (na linguagem que voce desejar, inclusive pode ser usando o Excel), ou seja concretize essa implementacao e mostre ela para os colegas em sala de aula ( no dia 31 de outubro ).
   4. Que texto inicial voce deveria incluir no seu programa para descrever se existe alguma restricao ao uso do mesmo ? (Por exemplo nao ser possivel ter f(x) com sinais positivos e negativos misturados ou qualquer outra coisa).
   5. Qual seria o erro esperado de uma integral calculada pela sua implementacao, devido ao metodo que voce escolheu para fazer a integracao numerica?
   6. Porque escolheu o Metodo que usou para implementar?
   Entregue as repostas aos itens 1, 2, 4, 5 e 6 por escrito no Classroom. Mostre seu programa em sala de aula dia 31 de outubro.
   Forma de avaliacao: Cada resposta correta vale ate 10 pontos na sua nota. Mostrar seu programa no dia 31 de outubro (vale ate 40 pontos). Ser criativo na sua apresentacao, no seu texto ou no seu programa vale mais ate 10 pontos.
   Entrega no Classroom - 31/10/2022 ;
   Apresentacao de cada um dos alunos ( aos demais alunos em sala ) 31/10/2022;
   Fechamento das Notas deste trabalho : 07/11/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



5. TRABALHO 5 - 2022 /2 - Ajuste de Curvas:
   
   Descobrir qual o melhor polinomio (reta ou curva) de determinado grau para representar um conjunto de pontos e' a aplicacao mais importante de ajuste de curvas. Neste trabalho voce vai fazer uma pesquisa sobre esse assunto, como se usa e programa o Metodo dos Minimo Quadrados para ajustar um polinomio a um conjunto de pontos minimizando o erro entre esse conjunto de pontos e a curva que os representara'. E vai apresentar o resultado desta pesquisa de 4 formas :
   1. Uma apresentacao em ppt do assunto;
   2. Um texto em pdf explicando o metodo dos minimos quadrados para fazer o ajuste dos pontos por uma curva de determinado aspecto;
   3. Um exemplo numerico resolvido por voce onde se determina uma curva por esse metodo para representar um dado conjunto de pontos;
   4. Procurar e indicar o link do melhor video que voce tenha assitido com a explicacao de como se faz esse ajuste ; e
   5. Uma apresentacao em sala para os colegas deste assunto.
   Entregue no Classroom e apresente a partir de 7/11 em sala de aula.
   Forma de avaliacao: Cada item vale ate' 2 pontos na sua nota.
   Data de apresentacao final e entrega no Classroom - 14/11/2022 ;
   Fechamento das Notas deste trabalho : 16/11/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .



---

Trabalhos 2022 / 1

1. TRABALHO 1 - 2022 :
   Depois de assistir os videos do TEMA 1 ( ler a bibliografia disponibilizada , procurar mais videos sobre o assunto e entender tudo muito bem) , escreva um texto de 3 ate 5 paginas, em que voce explica com suas palavras ( bem claro e concretamente ) os seguintes aspectos:
   1 - Como os numeros Reais ( da matematica ) sao representados como os numeros de "ponto flutuante" nos computadores digitais atuais.
   2 - Quais as formas possiveis deles serem aproximados ?
   3 - Porque a representacao deles como os numeros de "ponto flutuante" pode causar erros na comparacao com a solucao matematicamente correta mesmo em operacoes simples, feitas diversas vezes ( como somas e multiplicacoes consecutivas ) .
   4 - Para sua apresentacao de maneira concreta do item 3 apresente pelo menos 3 exemplos diferentes criados por voce mesmo, onde ocorre erro e calcule esses erros ( relativos e absolutos ) .
   5 - Junto com seu texto organize em uma apresentacao em forma de aula (em PPT) que leve de 5 a 15 minutos no maximo para ser assistida. Entregue tambem esse material em pdf no classroom
   
   Ate a data de entrega pode-se de tirar qualquer duvida sobre esse tema com a professora , nos horarios de aula ( ao vivo pela internet ) ou por e-mail.
   Entrega dos materiais desenvolvidos pelos alunos no Classroom - 06/04/2022 ;
Apresentacao das notas ( aos alunos em um xls ) em 11/04/2022 ;
Fechamento das Notas deste trabalho : 13/04/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



2. TRABALHO 2 - 2022 :
   Depois de assistir os videos do TEMA 2 ( e ler a bibliografia disponibilizada ) faca um video seu de 5 a 10 minutos onde voce:
   • Explica com um exemplo o Metodo de Newton-Raphson (NR) , como feito pela professora no video, mas usando outra funcao;
   • Faz uma explicacao clara dos conceitos basicos dos metodos anteriores (na ordem dos nossos videos);
   • Explica porque o metodo pode funcionar bem;
   • Diz em frases simples a ideia fundamental do criterio de convergencia deste metodo de NR.
   
   Entrega no Classroom - 20/04/2022 ; (Postar as contas que mostram o zero da funcao exemplo que usou e o video , se tiver usado outros materiais como um ppt auxiliar ou aulas e videos de outras fontes indique o link dessas referencias .)
   Fechamento das Notas deste trabalho : 25/04/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



3. TRABALHO 3 - 2022 :
   Existem duas grandes classes de metodos numericos para a resolucao de sistemas lineares. Os Metodos Diretos e os Metodos Iterativos. Nos Diretos a solucao ocorre por sua procura direta. Nos Iterativos se parte de uma aproximacao inicial para a solucao do sistema e gera-se uma sequencia de aproximacoes que se espera convirja para a solucao do sistema.
   Para entender bem ambos, escolha um sistema e o resolva por pelo menos um dos metodos Diretos e um dos metodos Iterativos apresentados nos videos deste Tema. Comente sua solucao em explicacoes escritas em um texto (como feito no capitulo 2 do texto do Prof. Marco Antonio ) ou em um video a ser entregue no classroom ate 27/04.

Entrega no Classroom - 27/04/2022 ; ( Postar o/os material/is mencionados )
Fechamento das Notas deste trabalho : 02/05/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



4. TRABALHO 4 - 2022 :
   Integrais definidas sao muito usadas para calcular areas entre uma curva e o sistema de eixos em que ela e' definida.
   Neste trabalho voce vai entender como fazer esse calculo numericamente , usando 3 metodos numericos diferentes (comentados nos videos do curso). Voce tambem vai conhecer bem a associacao entre: o numero de pontos usados neste calculo , o possivel erro de cada metodo e ainda se for dada uma tolerancia para a avaliacao da area como definir a quantidade de pontos que deve usar no calculo em cada caso .
   Ou seja seu trabalho consiste em entregar um texto em doc ou pdf em que calcule, explique o calculo feito e comente os detalhes ligados a :
   (1) calcular numericamente a area entre a funcao y = f ( x ) = e^x e o eixo hrizontal de x = 0 a x = 1 , pelos metodos :
   ( 1.1 ) Dos trapezios usando 10 pontos.
   ( 1.2 ) De Simpson usando 10 pontos.
   (2) Calcular o erro obtido em cada um dos metodos usando esses 10 pontos.
   (3) Calcular a mesma area pedida mas usando o metodo chamado de Quadratura de Gauss ou Quadratura Gaussiana com numero de pontos tais que voce tenha erros menores ou iguais a cada um dos metodos anteriores.
   (4) Responda as perguntas :
   (4.1) Para ter o mesmo erro pelos 3 metodos quantos pontos voce deveria usar nos 2 primeiros ?
   (4.1) Para fazer o calculo pela Quadratura de Gauss ou Quadratura Gaussiana em um intervalo diferente, por exemplo -1 a 3 , o que voce deveria fazer ?
   

   Entrega no Classroom - 11/05/2022 ; ( Postar o doc ou pdf mencionado )
   Fechamento das Notas deste trabalho : 16/05/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



5. TRABALHO Opcional - 2022 :
   Apos assistir os videos da Prof. Regina do Tema 4, e os abaixo:
   https://www.youtube.com/watch?v=I0jl27U6NqU
   https://www.youtube.com/watch?v=lno5xyQbIOU
   (que relembram a parte analitica dos sistemas de equacoes e a importancia do chute inicial) :
   1 - Resolva pelos Metodos de Newton-Raphson e Newton-Raphson Modificado o sistema:
   

   x + y = 2
   x² + y² = 4

   
   Usando na verificacao da convergencia a norma do maximo, ou sup, e uma tolerancia de 0,05. (Reveja o video de normas da Prof. Regina correspondente , caso tiver duvidas sobre essa norma) .
   2 - Indique na sua resposta em separado, claramente, as matrizes Jacobinas usadas em cada caso, e o que diferencia os dois metodos atraves de graficos (ou seja graficamente como os desenhos feitos pela Prof. Regina no video mencionado).
   3 - Apresente claramente como montou as formas iterativas do sistema e como achou o chute inicial dos valores de x e y .
   4 - Faca um video explicando de maneira clara e simples como resolveu o problema nao linear e, poste esse video no nosso classroom, alem da solucao pedida.

   Entrega no Classroom - 18/05/2022 ; ( Postar um pdf com os detalhes pedidos e o video mencionado )
   Fechamento das Notas deste trabalho : 23/05/2022 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---




---


turma 2021/2


Trabalhos 2021 / 2

1. TRABALHO 1 :
   Depois de assistir os videos do TEMA 1 ( ler a bibliografia disponibilizada , procurar mais sobre o assunto e entende-lo bem) fazer um pequeno video de ate 5 minutos , em que voce aparece como um entrevistado ( ou um professor ) explicando bem claro e concretamente porque o uso de numeros de "ponto flutuante" em operacoes , mesmo em simples somas, pode ser uma causa de erros em computacao numerica.
   Para sua apresentacao use algum material escrito por voce mesmo e organizado em uma apresentacao de PPT.
   
   DICAS:
   
   • Se tiver problemas em gravar, acesse o aplicativo de gravacao de videos Screencast O'Matic neste link : https://screencast-o-matic.com/register?ph=cYewir6zd ( Ele esta sendo Free mesmo ! E o mais simples fica sendo nem baixar , apenas se registrar e usar la , no proprio site deles ).
   
   
   • Outra dica: voce pode usar o proprio programa do ppt. As versoes mais recentes permitem voce tambem gravar sua apresentacao.
     
   
   
   • Ainda: se voce ainda lembrar do codigo de 10 letras de uma sala do Meet aberta (no primeiro ano da pandemia) em 2020, ela estava sem restricao de tempo e gravacao para todos, e pode usar essa sala para isto.
   
   Entrega do Video no Classroom - 28/10/2021 ;
Apresentacao ao vivo nas aulas ( a serem gravadas ) em 28/10/2021 e 2/11/2021 ;
Fechamento das Notas deste trabalho : 4/11/2021 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste item ) .

---



2. TRABALHO 2 :
   Depois de assistir os videos do TEMA 2 ( e ler a bibliografia disponibilizada ) fazer a moda antiga , com papel , lapis e borracha uma tabela com os passos pelo metodo da Falsa Posicao da busca pela raiz da funcao f ( x ) = x ln (x) - 3.2 contida no intervalo [ 2 , 3 ] com erro menor ou igual a 0.01 ou fazendo pelo menos 3 iteracoes. Comparando o seu resultado com o metodo anterior ( da Bissecao ) que conclusao (ou conclusoes) pode apontar ?
   Para sua entrega deste trabalho no classroom voce deve passar a sua solucao a limpo e congela-la de alguma forma (pode ser uma foto) e postar essa solucao como uma imagem jpg ou um arquivo pdf. Na sua nota vai ser levado em conta , alem de sua letra estar legivel e a tabela limpa e organizada, voce ter indicado claramente quais os passos desde metodo que voce usou para resolver o problema e chegar a resposta , ou seja: achar a raiz .
   
   DICA:
   
   • Se quizer voce pode usar como exemplo a resposta da busca da raiz desta funcao no texto disponibilizado no site "...professores.uff.br" p. 21 usar a forma como mostraram a solucao para o metodo da Bissecao , aqui agora para esse metodo.
     
   
   Entrega no Classroom - 09/11/2021 ;
   A segunda parte deste trabalho sera voce corrigir o trabalho que escolheu de um colega na data da entrega do mesmo, "congelar" e renviar essa correcao, ate o inicio da aula do dia 11/11/2021 !
   Fechamento das Notas deste trabalho : 11/11/2021 ( depois desta data nao sera possivel mais alteracoes da nota recebida neste trabalho ) .

---



3. TRABALHO 3 :
   Algumas vezes achar os determinates de matrizes tem muita utilidade , mas calcula-los pode ser bem complexo em especial para as ordens n x n com n maiores que 3.
   Depois de assistir os videos do TEMA 3 ( e ler a bibliografia disponibilizada ) principalmente as formas de solucao direta, o Metodo de Gauss e o seu algoritmo para a solucao de sistemas de equacoes lineares ( bastante comentado nestes materiais ) , implemente ( na linguagem de computacao que voce tiver mais dominio ) um programa ( didaticamente simples de entender ) para calcular o determinante de uma matriz 4 x 4 qualquer que o usuario forneca ao programa em tempo de execucao.
   Esse seu programa deve ser mostrado em codigo e executando para turma em ate 2 ( ou 3 ) minutos, individualmente, por cada aluno na aula de 23/11/2021 ( terca ) .
   DICA:
   
   • Lembre que o determinante pode ser sempre computado pela multiplicacao dos elementos de uma matriz triangular superior ou inferior, de qualquer ordem.
     
   
   Entrega no Classroom - 23/11/2021 ;
   Fechamento das Notas deste trabalho : 26/11/2021 .

---



4. TRABALHO 4 :
   Sabia que calcular "Sistemas nao-lineares" ou "zeros de funcoes vetoriais" tem mesmo significado . Nao ? Pois agora sabe !
   ( Brincadeirinha . . . . ;-) )
   Para continuarmos com esse bom humor mesmo as 7 horas da manha que tal uma aula com muitos professores criativos e divertidos ? Como conseguir esse "milagre" ? Vamos tentar juntos . . . .
   

   Depois de assistir os videos do TEMA 4 ( ler a bibliografia disponibilizada ) principalmente o primeiro video da Prof. Regina C. L. Toledo do tema, continue explicando a iteracao seguinte a ultima que ela mostra no video, continuando de onde ela parou ou ate atingir a tolerancia comentada, por ela, no inicio do exemplo. Faca isso na mesma forma "passo a passo" ( que ela explicou calmamente ) usando o Metodo de Newton-Raphson para encontrar a solucao do sistema :
   

   
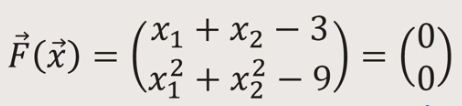
   Mas na sua apresentacao, se achar legal, "incorpore" algum personagem que voce esteja a vontade. Essa sua explicacao vai ser uma live (depois de virar o video) nesta nossa "rede social privada" do Classroom ( ou se preferir na Sala de Aula do Google ) de um "programa da serie" "Escolinha de Metodos Numericos do IC/UFF" de 2021 / 2 , onde cada aluno pode fazer de sua resposta um show de ate 2 minutos, na aula de 30/11/2021 ( terca ) .
   DICA:
   
   • Assista ate o fim a ultima aula gravada sobre Erros !
     
   
   Entrega no Classroom - 30/11/2021 ;
   Fechamento das Notas deste trabalho : 2/12/2021 .

---




5. TRABALHO 5 :
   Voce ja notou que cada trabalho motiva voce a aprender um dos temas do curso? O TEMA 5 sera' "Interpolacao polinomial" ou seja esse trabalho sera sobre o "Polinomio Interpolador de Lagrange" um dos metodos mais usados para isso .
   Nao sei se notou tambem que tentamos ser criativos quanto a forma dos trabalhos solicitados....
   Para esse trabalho vamos usar seu espirito de bom pesquisador ou detetive.
   Neste trabalho voce deve procurar materiais disponibilizados na www sobre o assunto de Interpolacao Polinomial de Lagrange e em especial videos (pode ser em ingles tambem) . A ideia e' voce nos mostrar em sala de aula o material que achou melhor e mais explicativo sobre algum aspecto deste assunto.
   Mas cuidado: se comunique com os colegas pois se houver video ou material repetido sendo indicado essa nota sera dividida entre os que o indicaram. Por exemplo: imagina que 3 alunos apontaram como mais intessante um mesmo material. Neste caso se o material for muito legal mesmo e valer 9, a nota de cada aluno sera no maximo 3.
   O material escolhido como o melhor de cada aluno sera mostrado para a turma a partir da aula de 7/12/2021. E pode levar mais de uma aula para vermos o unico material que cada aluno indicou na forma de um slide como um link no Classroom ( o aluno deve estar presente, para explicar porque achou esse o mais legal de todos os que viu, ao vivo na aula que sera gravada )
   
   Entrega no Classroom - 14/12/2021 ;
   Fechamento das Notas deste trabalho : 21/12/2021 .

---



6. TRABALHO 6 :
   Imagine que voce deseja descobrir a area entre x = [-10, 20] do polinomio:
   n₁ x¹ + n₂ x² + n₃ x³ + n4 x⁴ + n5 x⁵ + n6 x⁶ + n7 x⁷ +....
   Onde n₁ indica o numero de digitos no seu primeiro nome, n₂ indica o numero de digitos do seu segundo nome, n₃ do terceiro, n₄ do quarto, e assim por diante ate seu ultimo nome, use aqui seu nome completo. Ok?
   Por exemplo, no meu caso esse polinomio seria : P ( x ) = 4 x + 5 x² .
   Depois responda:
   Usando todos os seus nomes para geral o polinomio: Qual metodo numerico dentre os comentados nos videos voce escolheria para calcular essa area?
   Indique quantos intervalos voce usaria e de quanto deveria ser o intervalo usado para avaliar esse polinomio para descobrir essa area com erro menor que 1 milesimo por integracao numerica pelo metodo de Simpson e pelo Metodo dos Trapezios.
   

   Resolva numericamente essa area por 2 metodos diferentes e compare os erros.

   DICA:
   
   • Lembre das formulas de Gauss. Por elas para qualquer polinomio de grau g basta calcular a funcao a ser integrada em p pontos e usar os pesos tabelados para ter uma solucao com erro praticamente nenhum (sempre tem algum erro devido a truncagem dos numeros irracionais) ate g=2p+1. Assim vale bem a pena assistir o ultimo video do assunto da Prof. Regina ! !
     

   Entrega no Classroom - 04/01/2022 ;
   Fechamento das Notas deste trabalho : 06/01/2022 .

---

7. TRABALHO 7 :
   Imagine que voce deseja fazer um estudo explicando para pessoas que apenas lerao seu trabalho sobre a convergencia local e a estabilidade da solucao da EDO :
   y' = x - y + 2, y(0) = 2, x entre 0 e 1, quando resolvida por metodo de Runge-Kutta, e sabe que a solucao exata : y (x) = e^-x + x + 1 . Como voce resolveria esse desafio da melhor maneira possivel?
   DICA:
   
   • Assista os videos sobre EDO da Prof. Regina e leia o capitulo correspondente do texto: "Professores da UFF" !
     
   
   Entrega no Classroom - 11/01/2022 ;
   Fechamento das Notas deste trabalho : 13/01/2022 .

---

8. TRABALHO 8 :
   Nosso ultimo trabalho ! Ele sera sobre nosso ultimo tema: Ajuste de curvas.
   Tema super interessante que liga nosso curso a muitas aplicacoes importantissimas como por exemplo Fisica Experimental, Reconhecimento de Padroes, Sistemas Dinamicos, Computacao Grafica e Processamento de Imagens!
   Que tal voce descobrir mais sobre esse assunto maravilhoso do que apenas o ajuste mais conhecido e popular de todos (os Minimos quadrados) ?
   Assim, neste trabalho, vamos repetir a ideia do trabalho 5, onde voce nos apresentaram videos ou qualquer material sobre o assunto , os que achou bem interessantes.
   Comunicando-se com os demais colegas para nao se ter repeticao de forma alguma.
   Apenas nao pode isto (repetindo : de forma alguma ! ) Mais de um aluno apresentado o mesmo material....
   Entrega no Classroom - 18/01/2022 ;
   Fechamento das Notas deste trabalho : 20/01/2022 .



---



[Ementa] [Links] [Bibliografia] [Trabalhos] [Videos]


---

voltar inicio ementa ou Links

ver dados do professor

voltar linhas de pesquisa




---