Figure 4.2-1: Abstract model of a network
In order to transfer packets from a sending host to the destination
host, the network layer must determine the path or route
that the packets are to follow. Whether the network layer provides
a datagram service (in which case different packets between a given
host-destination pair may take different routes) or a virtual circuit service
(in which case all packets between a given source and destination will
take the same path), the network layer must nonetheless determine
the path for a packet. This is the job of the network layer routing
protocol.
At the heart of any routing protocol is the algorithm (the "routing algorithm") that determines the path for a packet. The purpose of a routing algorithm is simple: given a set of routers, with links connecting the routers, a routing algorithm finds a "good" path from source to destination. Typically, a "good" path is one which has "least cost," but we will see that in practice, "real-world" concerns such as policy issues (e.g., a rule such as "router X, belonging to organization Y should not forward any packets originating from the network owned by organization Z") also come into play to complicate the conceptually simple and elegant algorithms whose theory underlies the practice of routing in today's networks.
Figure 4.2-1: Abstract model of a network
The graph abstraction used to formulate routing algorithms is shown in Figure 4.2-1. (To view some graphs representing real network maps, see [Dodge 1999]; for a discussion of how well different graph-based models model the Internet, see [Zegura 1997]). Here, nodes in the graph represent routers - the points at which packet routing decisions are made - and the lines ("edges" in graph theory terminology) connecting these nodes represent the physical links between these routers. A link also has a value representing the "cost" of sending a packet across the link. The cost may reflect the level of congestion on that link (e.g., the current average delay for a packet across that link) or the physical distance traversed by that link (e.g., a transoceanic link might have a higher cost than a terrestrial link). For our current purposes, we will simply take the link costs as a given and won't worry about how they are determined.
Given the graph abstraction, the problem of finding the least cost path from a source to a destination requires identifying a series of links such that:
Only two types of routing algorithms are typically used in the Internet: a dynamic global link state algorithm, and a dynamic decentralized distance vector algorithm. We cover these algorithms in section 4.2.1 and 4.2.2 respectively. Other routing algorithms are surveyed briefly in section 4.2.3.
The link state algorithm we present below is known as Dijkstra's algorithm, named after its inventor (a closely related algorithm is Prim's algorithm; see [Corman 1990] for a general discussion of graph algorithms). It computes the least cost path from one node (the source, which we will refer to as A) to all other nodes in the network. Dijkstra's algorithm is iterative and has the property that after the kth iteration of the algorithm, the least cost paths are known to k destination nodes, and among the least cost paths to all destination nodes, these k path will have the k smallest costs. Let us define the following notation:
1 Initialization:
2 N = {A}
3 for all nodes v
4 if v adjacent to A
5 then D(v) = c(A,v)
6 else D(v) = infty
7
8 Loop
9 find w not in N such that D(w)
is a minimum
10 add w to N
11 update D(v) for all v adjacent to w and not
in N:
12 D(v) = min( D(v), D(w) +
c(w,v) )
13 /* new cost to v is either old cost to v or
known
14 shortest path cost to w plus cost from
w to v */
15 until all nodes in N
| step | N | D(B),p(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),p(F) |
| 0 | A | 2,A | 5,A | 1,A | infty | infty |
| 1 | AD | 2,A | 4,D | 2,D | infty | |
| 2 | ADE | 2,A | 3,E | 4,E | ||
| 3 | ADEB | 3E | 4E | |||
| 4 | ADEBC | 4E | ||||
| 5 | ADEBCF |
What is the computation complexity of this algorithm? That is, given n nodes (not counting the source), how much computation must be done in the worst case to find the least cost paths from the source to all destinations? In the first iteration, we need to search through all n nodes to determine the node, w, not in N that has the minimum cost. In the second iteration, we need to check n-1 nodes to determine the minimum cost; in the third iteration n-2 nodes and so on. Overall, the total number of nodes we need to search through over all the iterations is n*(n+1)/2, and thus we say that the above implementation of the link state algorithm has worst case complexity of order n squared: O(n2). (A more sophisticated implementation of this algorithm, using a data structure known as a heap, can find the minimum in line 9 in logarithmic rather than linear time, thus reducing the complexity).
Before completing our discussion of the LS algorithm, let us consider a pathology that can arise with the use of link state routing. Figure 4.2-2 shows a simple network topology where link costs are equal to the load carried on the link, e.g., reflecting the delay that would be experienced . In this example, link costs are not symmetric, i.e., c(A,B) equals c(B,A) only if the load carried on both directions on the AB link is the same. In this example, node D originates a unit of traffic destined for A, node B also originates a unit of traffic destined for A, and node C injects an amount of traffic equal to e, also destined for A. The initial routing is shown in Figure 4.2-2a, with the link costs corresponding to the amount of traffic carried.
When the LS algorithm is next run, node C determines (based on the link costs shown in Figure 4.2-2a) that the clockwise path to A has a cost of 1, while the counterclockwise path to A (which it had been using) has a cost of 1+e. Hence C's least cost path to A is now clockwise. Similarly, B determines that its new least cost path to A is also clockwise, resulting in the routing and resulting path costs shown in Figure 4.2-2b. When the LS algorithm is run next, nodes B, C and D all detect that a zero cost path to A in the counterclockwise direction and all route their traffic to the counterclockwise routes. The next time the LS algorithm is run, B, C, and D all then route their traffic to the clockwise routes.
What can be done to prevent such oscillations in the LS algorithm? One solution would be to mandate that link costs not depend on the amount of traffic carried -- an unacceptable solution since one goal of routing is to avoid highly congested (e.g., high delay) links. Another solution is to insure that all routers do not run the LS algorithm at the same time. This seems a more reasonable solution, since we would hope that even if routers run the LS algorithm with the same periodicity, the execution instants of the algorithm would not be the same at each node. Interestingly, researchers have recently noted that routers in the Internet can self-synchronize among themselves [Floyd 1994], i.e., even though they initially execute the algorithm with the same period but at different instants of time, the algorithm execution instants can eventually become, and remain, synchronized at the routers. One way to avoid such self-synchronization is to purposefully introduce randomization into the period between execution instants of the algorithm at each node.
Having now studied the link state algorithm, let's next consider the other major routing algorithm that is used in practice today - the distance vector routing algorithm.
The principal data structure in the DV algorithm is the distance table maintained at each node. Each node's distance table has a row for each destination in the network and a column for each of its directly attached neighbors. Consider a node X that is interested in routing to destination Y via its directly attached neighbor Z. Node X's distance table entry, Dx(Y,Z) is the sum of the cost of the direct one hop link between X and Z, c(X,Z), plus neighbor Z's currently known minimum cost path from itself (Z) to Y. That is:
Dx(Y,Z) = c(X,Z) + minw{Dz(Y,w)} (4-1)
The minw term in equation 4-1 is taken over all of Z's directly attached neighbors (including X, as we shall soon see).
Equation 4-1 suggests the form of the neighbor-to-neighbor communication that will take place in the DV algorithm -- each node must know the cost of each of its neighbors minimum cost path to each destination Thus, whenever a node computes a new minimum cost to some destination, it must inform its neighbors of this new minimum cost.
Before presenting the DV algorithm, let's consider an example that will help clarify the meaning of entries in the distance table. Consider the network topology and the distance table shown for node E in Figure 4.2-3. This is the distance table in node E once the Dv algorithm has converged. Let's first look at the row for destination A.
A circled entry in the distance table gives the cost of the least cost path to the corresponding destination (row). The column with the circled entry identifies the next node along the least cost path to the destination. Thus, a node's routing table (which indicates which outgoing link should be used to forward packets to a given destination) is easily constructed from the node's distance table.
In discussing the distance table entries for node E above, we informally took a global view, knowing the costs of all links in the network. The distance vector algorithm we will now present is decentralized and does not use such global information. Indeed, the only information a node will have are the costs of the links to its directly attached neighbors, and information it receives from these directly attached neighbors. The distance vector algorithm we will study is also known as the Bellman-Ford algorithm, after its inventors. It is used in many routing algorithms in practice, including: Internet BGP, ISO IDRP, Novell IPX, and the original ARPAnet.
Distance Vector (DV) Algorithm. At each node, X:
1 Initialization:
2 for all adjacent nodes v:
3 DX(*,v) = infty
/* the * operator means "for all rows" */
4 DX(v,v) = c(X,v)
5 for all destinations, y
6 send minwD(y,w) to each
neighbor /* w over all X's neighbors */
7
8 loop
9 wait (until I see a link cost change
to neighbor V
10 or until I receive
update from neighbor V)
11
12 if (c(X,V) changes by d)
13 /* change cost to all dest's via
neighbor v by d */
14 /* note: d could be positive or negative
*/
15 for all destinations y: DX(y,V)
= DX(y,V) + d
16
17 else if (update received from V wrt
destination Y)
18 /* shortest path from V to some Y
has changed */
19 /* V has sent a new value for its
minw DV(Y,w) */
20 /* call this received new value is
"newval" */
21 for the single destination y: DX(Y,V)
= c(X,V) + newval
22
23 if we have a new minw DX(Y,w)for
any destination Y
24 send new value of minw
DX(Y,w) to all neighbors
25
26 forever
The key steps are lines 15 and 21, where a node updates its distance table entries in response to either a change of cost of an attached link or the receipt of an update message from a neighbor. The other key step is line 24, where a node sends an update to its neighbors if its minimum cost path to a destination has changed.
Figure 4.2-4 illustrates the operation of the DV algorithm for the simple three node network shown at the top of the figure. The operation of the algorithm is illustrated in a synchronous manner, where all nodes simultaneously receive messages from their neighbors, compute new distance table entries, and inform their neighbors of any changes in their new least path costs. After studying this example, you should convince yourself that the algorithm operates correctly in an asynchronous manner as well, with node computations and update generation/reception occurring at any times.
The circled distance table entries in Figure 4.2-4 show the current least path cost to a destination. An entry circled in red indicates that a new minimum cost has been computed (in either line 4 of the DV algorithm (initialization) or line 21). In such cases an update message will be sent (line 24 of the DV algorithm) to the node's neighbors as represented by the red arrows between columns in Figure 4.2-4.
Figure 4.2-4: Distance Vector Algorithm: example
The leftmost column in Figure 4.2-4 shows the distance table entries for nodes X, Y, and Z after the initialization step.
Let us now consider how node X computes the distance table shown in the middle column of Figure 4.2-4 after receiving updates from nodes Y and Z. As a result of receiving the updates from Y and Z, X computes in line 21 of the DV algorithm:
The value DX(Z,Y) = 3 means that X's minimum cost to Z has changed from 7 to 3. Hence, X sends updates to Y and Z informing them of this new least cost to Z. Note that X need not update Y and Z about its cost to Y since this has not changed. Note also that Y's recomputation of its distance table in the middle column of Figure 4.2-4 does result in new distance entries, but does not result in a change of Y's least cost path to nodes X and Z. Hence Y does not send updates to X and Z.
The process of receiving updated costs from neighbors, recomputation
of distance table entries, and updating neighbors of changed costs of the
least cost path to a destination continues until no update messages are
sent. At this point, since no update messages are sent, no further
distance table calculations will occur and the algorithm enters a quiescent
state, i.e., all nodes are performing the wait in line 9 of the DV algorithm.
The algorithm would remain in the quiescent state until a link cost
changes, as discussed below.
In Figure 4.2-5, only two iterations are required for the DV algorithm to reach a quiescent state. The "good news" about the decreased cost between X and Y has propagated fast through the network.
Let's now consider what can happen when a link cost increases. Suppose that the link cost between X and Y increases from 4 to 60.
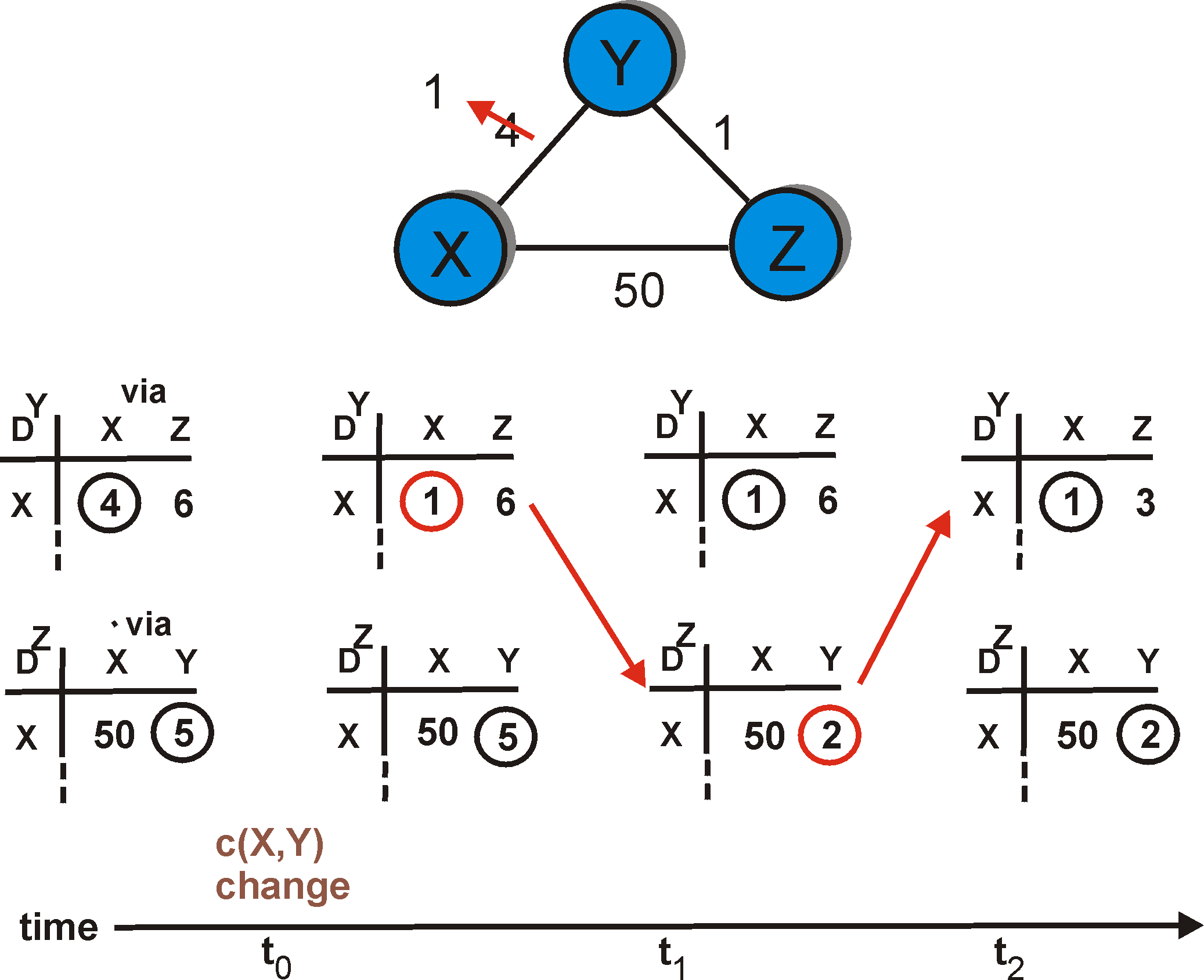
Figure 4.2-6: Link cost changes: bad news travels slow and causes
loops
Figure 4.2-7 illustrates how poisoned reverse solves the particular looping problem we encountered before in Figure 4.2-6. As a result of the poisoned reverse, Y's distance table indicates an infinite cost when routing to X via Z (the result of Z having informed Y that Z's cost to X was infinity). When the cost of the XY link changes from 4 to 60 at time t0, Y updates its table and continues to route directly to X, albeit at a higher cost of 60, and informs Z of this change in cost. After receiving the update at t1, Z immediately shifts it route to X to be via the direct ZX link at a cost of 50. Since this is a new least cost to X, and since the path no longer passes through Y, Z informs Y of this new least cost path to X at t2. After receiving the update from Z, Y updates its distance table to route to X via Z at a least cost of 51. Also, since Z is now on Y's least path to X, Y poisons the reverse path from Z to X by informing Z at time t3 that it (Y) has an infinite cost to get to X. The algorithm becomes quiescent after t4, with distance table entries for destination X shown in the rightmost column in Figure 4.2-7.
Does poison reverse solve the general count-to-infinity problem?
It does not. You should convince yourself that loops involving
three or more nodes (rather than simply two immediately neighboring
nodes, as we saw in Figure 4.2-7) will not be detected by the poison reverse
technique.
Nonetheless, many routing algorithms have been proposed by researchers over the past 30 years, ranging from the extremely simple to the very sophisticated and complex. One of the simplest routing algorithms proposed is hot potato routing. The algorithm derives its name from its behavior -- a router tries to get rid of (forward) an outgoing packet as soon as it can. It does so by forwarding it on any outgoing link that is not congested, regardless of destination. Although initially proposed quite some time ago, interest in hot-potato-like routing has recently been revived for routing in highly structured networks, such as the so-called Manhattan street network [Brassil 1994].
Another broad class of routing algorithms are based on viewing packet traffic as flows between sources and destinations in a network. In this approach, the routing problem can be formulated mathematically as a constrained optimization problem known as a network flow problem [Bertsekas 1991]. Let us define l ij as the amount of traffic (e.g., in packets/sec) entering the network for the first time at node i and destined for node j. The set of flows, {l ij} for all i,j, is sometimes referred to as the network traffic matrix. In a network flow problem, traffic flows must be assigned to a set of network links subject to constraints such as:
But what performance function should be optimized? There are many possible choices. If we make certain assumptions about the size of packets and the manner in which packets arrive at the various routers, we can use the so-called M/M/1 queueing theory formula [Kleinrock 1976] to express the average delay at linkas:
Dm = 1 / (Rm - SiSj l ijm),
where Rm is link m's capacity (measured in terms of the average number of packets/sec it can transmit) and SiSj l ijm is the total arrival rate of packets (in packets/sec) that arrive to link m. The overall network wide performance measure to be optimized might then be the sum of all link delays in the network, or some other suitable performance metric. A number of elegant distributed algorithms exist for computing the optimum link flows (and hence routing determine the routing paths, as discussed above). The reader is referred to [Bertsekas 1991] for a detailed study of these algorithms.
The final set of routing algorithms we mention here are those derived from the telephony world. These circuit-switched routing algorithms are of interest to packet-switched data networking in cases where per-link resources (e.g., buffers, or a fraction of the link bandwidth) are to reserved (i.e., set aside) for each connection that is routed over the link. While the formulation of the routing problem might appear quite different from the least cost routing formulation we have seen in this chapter, we will see that there are a number of similarities, at least as far as the path finding algorithm (routing algorithm) is concerned. Our goal here is to provide a brief introduction for this class of routing algorithms. The reader is referred to [Ash 1998],[Ross 1995], [Girard 1990] for a detailed discussion of this active research area.
The circuit-switched routing problem formulation is illustrated in Figure 4.2-8. Each link has a certain amount of resources (e.g., bandwidth). The easiest (and a quite accurate) way to visualize this is to consider the link to be a bundle of circuits, with each call that is routed over the link requiring the dedicated use of one of the link's circuits. A link is thus characterized both by its total number of circuits, as well as the number of these circuits currently in use. In Figure 4.2-8, all links except AB and BD have 20 circuits; the number to the left of the number of circuits indicates the number of circuits currently in use.
Suppose now that a call arrives at node A, destined to node D. What path should be take? In shortest path first (SPF) routing, the shortest path (least number of links traversed) is taken. We have already seen how the Dijkstra LS algorithm can be used to find shortest path routes. In Figure 4.2-8, either that ABD or ACD path would thus be taken. In least loaded path (LLP) routing, the load at a link is defined as the ratio of the number of used circuits at the link and the total number of circuits at that link. The path load is the maximum of the loads of all links in the path. In LLP routing, the path taken is that with the smallest path load. In example 4.2-8, the LLP path is ABCD. In maximum free circuit (MFC) routing, the number of free circuits associated with a path is the minimum of the number of free circuits at each of the links on a path. In MFC routing, the path the maximum number of free circuits is taken. In Figure 4.2-8 the path ABD would be taken with MFC routing.
Given these examples from the circuit switching world, we see that the
path selection algorithms have much the same flavor as LS routing.
All nodes have complete information about the network's link states.
Note however, that the potential consequences of old or inaccurate sate
information are more severe with circuit-oriented routing -- a call may
be routed along a path only to find that the circuits it had been expecting
to be allocated are no longer available. In such a case, the call
setup is blocked and another path must be attempted. Nonetheless, the main
differences between connection-oriented, circuit-switched routing and connectionless
packet-switched routing come not in the path selection mechanism, but rather
in the actions that must be taken when a connection is set up, or torn
down, from source to destination.
Copyright Keith W. Ross and James F. Kurose, 1996-2000. All rights reserved.