o A contribuição dos megáricos e estóicos
o Euclides e o Método Axiomático
o Diophantus e o desenvolvimento da Álgebra
o A automatização do raciocínio
o Leibniz, o precursor da Lógica Matemática moderna
§
A lógica matemática no século
XIX
§
Boole e os fundamentos da
Lógica Matemática e da Computação
o A importância de Frege e Peano
o O desenvolvimento da Lógica Matemática
§
A crise dos fundamentos e as
tentativas de superação
§
Kurt Gödel: muito além da
lógica
§
Alan Mathison Turing: o berço
da Computação
o O problema da parada e o problema da decisão
o A tese de Church-Turing e outros resultados teóricos
§ Notas
Considerando
as idéias e os conceitos como uma das linhas que conduzirão ao grande desenvolvimento
tecnológico da Computação a partir da década de 40 do século XX, este capítulo
fará referência a alguns aspectos da evolução da Ciência da Matemática, mais
especificamente de alguns dos seus ramos, no caso a Álgebra e a Lógica
Simbólica ou Matemática, de onde nos vieram o rigor e o método axiomático, até
chegar na noção de computabilidade e procedimento, com Turing.
Os primeiros
passos em direção aos computadores digitais foram dados no Egito e na
Babilônia, há mais de quatro milênios, com os sistemas de medidas de distâncias
e previsão do curso das estrelas. Durante a civilização grega estas
pré-ciências tomaram forma através dos sistemas axiomáticos§1.
Talvez o
passo mais fundamental dado nestes primeiros tempos tenha sido a compreensão do
conceito de número, quer dizer, ver o número não como uma maneira de se
poder contar, mas como uma idéia abstrata. Não está registrado como deve ter
sido o reconhecimento, pelos nossos antepassados mais primitivos, de que quatro
pássaros caçados eram distintos de dois, assim como o passo nada elementar de
associar o número quatro, relativo a quatro pássaros, e o número quatro,
associado a quatro pedras.
A visão
do número como uma qualidade de um determinado objeto é um obstáculo ao
desenvolvimento de uma idéia verdadeira de número. Somente quando, de acordo
com o nosso exemplo, o número quatro foi dissociado dos pássaros ou das pedras
tornando-se uma entidade independente de qualquer objeto - uma abstração, como
diriam os filósofos - é que se pôde dar o primeiro passo em direção a um
sistema de notação, e daí para a aritmética. Conforme Bertrand Russell, "foram
necessários muitos anos para se descobrir que um par de faisões e um par de
dias eram ambos instâncias do número dois"[Dan54].
Uma
primeira cronologia que se pode estabelecer é a que vai do ano 4.200 a.C. até
meados do ano 1600 d.C. Um museu em Oxford possui um cetro egípcio de mais de
5.000 anos, sobre o qual aparecem registros de 120.000 prisioneiros e 1.422.000
cabras capturadas[Boy74] .
Apesar do exagero dos números, fica claro que os egípcios procuravam ser
precisos no contar e no medir, bastando lembrar o alto grau de precisão das
pirâmides. As primeiras tentativas de invenção de dispositivos mecânicos para
ajudar a fazer cálculos datam dessas épocas, como por exemplo o ábaco e o
mecanismo Antikythera, sobre os quais se falará mais detidamente no capítulo da
Pré-História Tecnológica.
Sob o
foco que se está trabalhando, deve-se ver nestes tempos as tentativas de
conceituação do número, o estabelecimento das bases numéricas, o estudo da
Álgebra e geometria que tanto atraíram os antigos. Tempos de evolução lenta, e
em termos de produção efetiva de conhecimento matemático bem abaixo da
quantidade e qualidade produzida quase que exponencialmente a partir do século XV
d.C., mas não menos importantes. De fato, para se compreender a História da
Matemática na Europa é necessário conhecer sua história na Mesopotâmia e Egito,
na Grécia antiga e na civilização islâmica dos séculos IX a XV.
A Lógica
foi considerada na tradição clássica e medieval como instrumento indispensável
ao pensamento científico. Atualmente é parte importante na metodologia dedutiva
das ciências, além de constituir-se como um saber próprio, com abertura a
relevantes problemas teoréticos. Da Ciência Lógica nasceu a Lógica Matemática
e, dentro desta, várias filosofias da lógica que interpretam os cálculos
simbólicos e sua sistematização axiomática. Para a História da Computação
interessa abordar em particular a questão do pensamento dedutivo e matemático,
seus limites, o problema da relativa mecanização do pensamento quantitativo e o
problema da Inteligência Artificial. Da discusssão e busca da solução desses
problemas, que entram também no campo filosófico, formou-se a base conceitual,
Teoria da Computabilidade, necessária para o advento do computadores.
O início
da ciência da Lógica encontra-se na antiga Grécia [Kne68] [Boc66]. As polêmicas geradas
pela teoria de Parmênides e os famosos argumentos de Zenão §2, que negavam a realidade
do movimento fazendo um uso indevido do princípio da não-contradição, contribuiram
para a distinção dos conceitos, para se ver a necessidade de argumentar com
clareza mediante demonstrações rigorosas, respondendo às objeções dos
adversários. Mais tarde, as sutilezas dos sofistas, que reduziam todo o
saber à arte de convencer pelas palavras, levaram Sócrates a defender o valor
dos conceitos e tentar defini-los com precisão. Assim a Lógica como ciência vai
se formando pouco a pouco, principalmente com Sócrates e Platão. Mas Platão
pensava que qualquer conteúdo da mente existia tal qual na realidade e
Aristóteles reage ao seu mestre, dizendo que as idéias existem somente na mente
humana, mas correspondendo a realidades.
O início
da ciência da Lógica encontra-se na antiga Grécia [Kne68] [Boc66]. As polêmicas
geradas pela teoria de Parmênides e os famosos argumentos de Zenão , que
negavam a realidade do movimento fazendo um uso indevido do princípio da
não-contradição, contribuíram para a distinção dos conceitos, para se ver a
necessidade de argumentar com clareza, mediante demonstrações rigorosas, e
assim responder às objeções dos adversários. Mais tarde, as sutilezas dos
sofistas, que reduziam todo o saber à arte de convencer pelas palavras, levaram
Sócrates a defender o valor dos conceitos e tentar defini-los com precisão.
Assim a Lógica como ciência vai se formando pouco a pouco, principalmente com
Sócrates e Platão. Mas Platão pensava que qualquer conteúdo da mente existia
tal qual na realidade e Aristóteles reage ao seu mestre, dizendo que as idéias
existem somente na mente humana, mas correspondendo a realidades.
Com
Aristóteles é que se dá o verdadeiro nascimento da Lógica como ciência das
idéias e dos processos da mente. "Até hoje não existe forma alguma
concebível de lógica, por muito distinta que seja da lógica formal, que não
tenha algum tipo de conexão com a obra aristotélica" [Sch31]. Ele foi o primeiro
lógico formal da história, tendo desenvolvido ao menos duas formas distintas de
lógica formal, elaborando algumas de suas partes de maneira praticamente
completa e deixando esboçados outros tipos de lógicas que somente na época
atual foram novamente tratadas§3 .
Aristóteles
escreveu uma série de trabalhos que seriam editados por Andrônico de Rodes no
século I d.C. e que receberam posteriormente o nome de Organon
("Instrumento"), de acordo com a concepção segundo a qual a Lógica
deveria fornecer os instrumentos mentais necessários para enfrentar qualquer tipo
de investigação. Essa obra compreende os seguintes livros: Categorias,
Analíticos I, Analíticos II, o Peri Hermeneias (ou sobre a interpretação),
Tópicos e Refutação de argumentos sofistas. A grande novidade aristotélica está
nos Analíticos, com o silogismo. Aristóteles chamava a Lógica com o termo
"analítica" (e justamente "Analíticos" são intitulados os
escritos fundamentais do Organon). A analítica (do grego analysis, que
significa "resolução") explica o método pelo qual, partindo de uma
dada conclusão, resolve-se precisamente nos elementos dos quais deriva, isto é,
nas premissas e nos elementos de que brota, e assim fica fundamentada e
justificada.
Aristóteles construiu uma sofisticada teoria dos argumentos, cujo núcleo é a
caracterização e análise dos chamados silogismos, os típicos raciocínios da
lógica aristotélica. O argumento
Todo
homem é mortal
Sócrates
é homem
Logo
Sócrates é mortal
é o
exemplo típico do silogismo perfeito.Conforme o próprio Aristóteles, "o silogismo
é um discurso no qual, sendo admitidas algumas coisas, outra coisa distinta
resulta necessariamente dessas coisas afirmadas primeiro, pelo único fato de
que essas existem" [Per88].
Nos
Primeiros Analíticos, Aristóteles desenvolveu minuciosamente o sistema dos
silogismos, mostrando os princípios maiores que o sustentam e as regras que lhe
devem moldar a construção. A análise do Filósofo é tão ampla quanto engenhosa e
envolve também as assim chamadas "modalidades" e os silogismos modais§4.
Entre as
características mais importantes da silogística aristotélica está a de se ter
pensado pela primeira vez na história da lógica em fazer uso de letras que
poderiam ser usadas para uma expressão substantiva qualquer, fundamental para
desenvolvimentos posteriores. É também com Aristóteles que se encontra uma das
primeiras tentativas de se estabelecer um rigor nas demonstrações matemáticas.
Ao definir os dois tipos de demonstração, quia (dos efeitos às causas) e
propter quid (das causas aos efeitos), dizia (I Anal. Post., lect. 14)
que as matemáticas utilizam preferencialmente esse modo de demonstrar, e por
isso esta ciência é essencialmente dedutiva: "algumas vezes o mais
conhecido por nós em si mesmo e por natureza é também o mais cognoscível em si
mesmo e por natureza. Assim acontece nas matemáticas, nas quais, devido à
abstração da matéria, não se efetuam demonstrações mais do que a partir dos
princípios formais. E assim as demonstrações procedem desde o mais cognoscível
em si mesmo".
A contribuição dos megáricos e estóicos
Embora
Aristóteles seja o mais brilhante e influente filósofo grego, outra importante
tradição argumentativa formou-se na antiga Grécia, com os megáricos e estóicos.
Pouco conservada pela tradição, merece um melhor tratamento dos historiadores,
porque o pouco que se conhece sugere que esses gregos eram altamente
inteligentes.
Os
megáricos (em função de sua cidade, Mégara) interessaram-se por certos enigmas
lógicos como o conhecido "paradoxo do mentiroso": quem diz "O
que eu afirmo agora é falso", enuncia algo verdadeiro ou falso? Um deles,
Diodoro Cronus, que morreu por volta de 307 a.C., formulou interessante concepção
modal, relacionando possibilidade, tempo e verdade, enquanto outro megárico, de
nome Fílon, estudou proposições do tipo "Se chove então a rua está
molhada", contruída com o auxílio das expressões "se...,
então..." conhecidas como condicionais. Ele as definiu em termos extremamente
polêmicos, mas que seriam assumidos como corretos, vinte e três séculos mais
tarde pelos fundadores da Lógica Contemporânea.
Os
estóicos (da chamada escola filosófica de "Stoa", que quer dizer
"pórtico") desenvolveram também notáveis teorias lógicas. Tinham
bastante presente a diferença que há entre um código de comunicação específico,
de um lado, e o que se pode expressar através do uso de tal código. Assim
sendo, um conceito de "proposição" análogo ao usado na atual Lógica,
já estava presente, de modo virtual, na filosofia estóica da linguagem.
Porém a
mais notável contribuição estóica à Lógica foi obra de Crísipo de Soles
(280-206 a.C.), homem de vasta produção poligráfica (750 livros). Ele estudou
as sentenças condicionais e também as disjuntivas (regidas pela
partícula "ou") e as copulativas (regidas pelo "e"), tendo
também reconhecido claramente o papel lógico desempenhado pela negação. Além
disto, Crísipo foi capaz de relacionar tais idéias com as modalidades,
elaborando, então, um sistema de princípios lógicos que, no seu campo
específico, foi muito além dos poucos resultados obtidos por Aristóteles e seu
discípulo Teofrasto. Por tal razão, Crísipo é reconhecido como o grande
precursor daquilo que hoje se chama "Cálculo Proposicional", o
primeiro capítulo da Lógica desenvolvida a partir do último quarto do século
XIX [Bri79b].
Euclides e o Método Axiomático
Com sua
obra Elementos, o matemático grego Euclides (330 a 277 a.C.
aproximadamente) deu forma sistemática ao saber geométrico. No primeiro livro
dos Elementos, ele enuncia vinte e três definições, cinco postulados e algumas
noções comuns ou axiomas§5. Em seguida ele deduz proposições ou teoremas, os
quais constituem o saber geométrico, como por exemplo: "se em um triângulo
dois ângulos são iguais entre si, também os lados opostos a esses ângulos são
iguais entre si".
Esse é
portanto o modo como Euclides ordena o conhecimento geométrico no chamado
sistema euclidiano. Durante séculos esse sistema valeu como modelo insuperável
do saber dedutivo: os termos da teoria são introduzidos depois de terem sido
definidos e as proposições não são aceitas se não foram demonstradas. As proposições
primitivas, base da cadeia sobre a qual se desenvolvem as deduções
sucessivas, Euclides as escolhia de tal modo que ninguém pudesse levantar
dúvidas sobre a sua veracidade: eram auto-evidentes, portanto isentas de
demonstração. Leibniz afirmaria mais tarde que os gregos raciocinavam com toda
a exatidão possível em matemática e deixaram à humanidade modelos de arte
demonstrativa([RA91], volume III).
Em
resumo, Euclides, como já fizera Aristóteles, buscou o ideal de uma organização
axiomática, que em última instância se reduz à escolha de um pequeno número de
proposições notoriamente verdadeiras daquele domínio do conhecimento, e à
posterior dedução de todas as outras proposições verdadeiras desse domínio, a
partir delas.
Surge
com Euclides e Aristóteles (estará plenamente desenvolvida no início do século
XX com a escola formalista de Hilbert) a busca de uma economia do pensamento
(um bom texto sobre o assunto pode ser encontrado em [Wil65]). A História da
Computação tem um marco significativo nesse ponto da História: o começo da
busca da automatização do raciocínio e do cálculo.
Mas
havia um problema no sistema de Euclides: suas "evidências" não eram
assim tão evidentes. O seu quinto postulado não convenceu de modo algum, e
despertou perplexidade na história do próprio pensamento grego, depois no árabe
e no renascentista. No século XIX, Karl Friedrich Gauss (1777-1855) viu com
toda a clareza a não demonstrabilidade do quinto postulado e a possibilidade da
construção de sistemas geométricos não euclidianos. Janos Boulay (1802-1860),
húngaro, e Nicolai Ivanovic Lobacewskiy (1793-1856), russo, trabalhando
independentemente, constróem uma geometria na qual o postulado da paralela não
vale mais.
A
consequência desses fatos foi a eliminação dos poderes da intuição na
fundamentação e elaboração de uma teoria geométrica: os axiomas não são mais
"verdades evidentes" que garantem a "fundação" do sistema
geométrico, mas puros e simples pontos de partida, escolhidos convencionalmente
para realizar uma construção dedutiva. Mas, se os axiomas são puros pontos de
partida, quem garantirá que, continuando-se a deduzir teoremas, não se cairá em
contradição?
Esta
questão crucial dos fundamentos da matemática levará aos grandes estudos dos
finais do século XIX e inícios do XX e será o ponto de partida do projeto
formalista de David Hilbert, assim como de outras tentativas de se fundamentar
a matemática na lógica e na teoria dos conjuntos, como as propostas por Frege,
Russell e Cantor. Mas será dessa sequência de sucessos e fracassos que se
produzirá a base da Computação, com Turing, von Neumann, Post, Church, e outros
mais.
Diophantus e o desenvolvimento da Álgebra
O
seguinte problema no Rhind Papyrus, do Museu britânico em Londres, foi
escrito por volta do ano 1650 a.C.:
Divida
100 pães entre 10 homens, incluindo um barqueiro, um capataz e um vigia, os
quais recebem uma dupla porção cada. Quanto cabe a cada um? [Bow94]
Isto
naturalmente pode ser resolvido usando-se Álgebra.
O
primeiro tratado de Álgebra foi escrito pelo grego Diophantus, da cidade de
Alexandria, por volta do ano 250. O seu Arithmetica, composto
originalmente por 13 livros dos quais somente 6 se preservaram, era um tratado
"caracterizado por um alto grau de habilidade matemática e de engenho:
quanto a isto, o livro pode ser comparado aos grandes clássicos da idade
alexandrina anterior" [Boy74].
Antes de Diophantus, toda a 'álgebra' que havia, incluindo problemas,
operações, lógica e solução, era expressada sem simbolismo - palavra
chave sobre a qual ainda se voltará a falar - ; ele foi o primeiro a introduzir
o simbolismo na matemática grega. Para uma quantidade desconhecida usava um
símbolo (chamado arithmos), que caracterizava um número indefinido de
unidades. Pela ênfase dada em seu tratado à solução de problemas
indeterminados, tal tratado tornou-se conhecido como análise diofantina,
em geral parte de cursos de teoria dos números§6. Seu trabalho, contudo,
não é suficiente para lhe conferir o título de pai da Álgebra§7.
Mas é
com os persas e principalmente com os árabes que a Álgebra poderá ser
efetivamente chamada de ciência. É interessante notar que ao se falar que a Geometria
é uma ciência grega ou que a Álgebra é uma ciência árabe, está se afirmando
algo mais do que a "casualidade" de terem sido gregos ou árabes seus
fundadores ou promotores. Ordinariamente tendemos a pensar que o conhecimento
científico independe de latitudes e culturas: uma fórmula química ou um teorema
de Geometria são os mesmos em inglês ou português ou chinês e, sendo a
comunicação, à primeira vista, o único problema, bastaria uma boa tradução dos
termos próprios de cada disciplina. Mas não é assim.
Na
verdade a evolução da ciência está repleta de interferências
histórico-culturais, condicionando metodologias, o surgimento de novas áreas do
saber, e assim por diante. Os juristas árabes referem-se à Álgebra como "o
cálculo da herança", segundo a lei corânica, uma problemática importante
dentro do Islam, e aí já temos um exemplo de condicionamento
histórico-cultural. Não foi por mero acaso que a Álgebra surgiu no califado
abássida ("ao contrário dos Omíadas, os Abássidas pretendem aplicar rigorosamente
a lei religiosa à vida cotidiana" [AG81]),
no seio da "Casa da Sabedoria" (Bayt al-Hikma) de Bagdá, promovida
pelo califa Al-Ma'amun; uma ciência nascida em língua árabe e antagônica da
ciência grega. Embora hoje a Álgebra possa parecer objetiva e axiomática, com
uma sintaxe de estruturas operatórias e destituída de qualquer alcance
semântico, ela é o resultado da evolução da velha al'jabr, "forjada por um
contexto cultural em que não são alheios elementos que vão desde as estruturas
gramaticais do árabe à teologia muçulmana da época" [Lau97].
Muhammad Ibn Musa Al-Khwarizmi (780 - 850), matemático e astrônomo persa, foi
membro da "Casa da Sabedoria", a importante academia científica de
Bagdá, que alcançou seu resplendor com Al-Ma'amun (califa de 813 a 833). A ele,
Al-Khwarizmi (imagem) dedicou seu Al-Kitab al-muhtasar fy hisab al-jabr
wa al-muqabalah ("Livro breve para o cálculo da jabr e da
muqabalah"). Al-jabr, que significa força que obriga, restabelecer ,
precisamente porque a Álgebra é "forçar cada termo a ocupar seu devido
lugar". Já no começo do seu Kitab, Al-Khwarizmi distingue seis formas de
equação, às quais toda equação pode ser reduzida (e, canonicamente resolvida).
Na notação atual:
1. ax2 = bx
2. ax2 = c
3. ax = c
4. ax2 + bx = c
5. ax2 + x = ax2
6. bx + c = ax2
Al-jabr é a operação que soma um mesmo fator (afetado do sinal +) a ambos os
membros de uma equação, para eliminar um fator afetado pelo sinal -. Já a
operação que elimina termos iguais de ambos os lados da equação é al-muqabalah
que significa estar de frente, cara a cara, confrontar. Por exemplo: em um
problema onde os dados podem ser colocados sob a forma 2x2 + 100 - 20x = 58,
Al-Khwarizmi procede do seguinte modo:
2x2 + 100 = 58 + 20x (por al-jabr)
Divide
por 2 e reduz os termos semelhantes:
x2 + 21 = 10 x (por al-muqabalah)
E o
problema já está canonicamente equacionado.
Al-Kharazmi
introduziu a escrita dos cálculos no lugar do uso do ábaco. De seu nome
derivaram as palavras, como já citado acima na história do desenvolvimento do
conceito de número, algarismo e algoritmo§8 [Kar61].
Embora
não muito visível ainda, deve-se chamar a atenção para essa disciplina da
Álgebra, que deve ser colocada entre as ciências que fundamentaram o
desenvolvimento da Computação. Pois o computador e todos os instrumentos que o
precederam (réguas de cálculo, máquina de Pascal, a calculadora de Leibniz, a
máquina analítica de Babbage, etc.) são somente as manifestações práticas que
foram surgindo, com naturalidade, em resultado da busca pelo homem de reduzir
os problemas a expressões matemáticas, resolvendo-as segundo regras. E isto, há
muitos séculos, já tinha tomado o nome de Álgebra, a "arte dos raciocínios
perfeitos" como dizia Bhaskara, o conhecido matemático hindu do século
XII. Com os árabes, depois de relativo obscurecimento da cultura grega, dá-se
continuidade ao processo que proporcionará as bases fundamentais para o
raciocínio automatizado, fundamental na Ciência da Computação.
Ainda
dentro do período acima estabelecido (4.200 a.C. até meados do ano 1600 d.C)
iniciou-se concretização de uma antiga meta: a idéia de se reduzir todo
raciocínio a um processo mecânico, baseado em algum tipo de cálculo formal.
Isto remonta a Raimundo Lúlio. Embora negligenciado pela ciência moderna,
Raimundo Lúlio (1235-1316), espanhol, figura pletórica de seu tempo, em seu
trabalho Ars Magna (1305-1308), apresentou a primeira tentativa de um
procedimento mecânico para produzir sentenças logicamente corretas [Her69] . Lúlio acreditava que
tinha encontrado um método que permitia, entre outras coisas, tirar todo tipo
de conclusões, mediante um sistema de anéis circulares dispostos
concentricamente, de diferentes tamanhos e graduáveis entre si, com letras em
suas bordas. Invenção única, tentará cobrir e gerar, representando com letras -
que seriam categorias do conhecimento - , todo o saber humano,
sistematizado em uma gramática lógica.
Conforme
Hegel: "A tendência fundamental da 'arte' de Raimundo Lúlio consistia em
enumerar e ordenar todas as determinações conceituais a que era possível
reduzir todos os objetos, as categorias puras com referência às quais podiam
ser determinados, para, desse modo, poder assinalar facilmente, com respeito a
cada objeto, os conceitos a ele aplicáveis. Raimundo Lúlio é, pois, um pensador
sistemático, ainda que ao mesmo tempo mecânico. Deixou traçada uma tabela em
círculos nos quais se acham inscritos triângulos cortados por outros círculos.
Dentro desses círculos, ordenava as determinações conceituais, com pretensões
exaustivas; uma parte dos círculos é imóvel, a outra tem movimento. Vemos, com
efeito, seis círculos, dois dos quais indicam os sujeitos, três os predicados e
o sexto as possíveis perguntas. Dedica nove determinações a classe,
designando-as com as nove letras B C D E F G H I K. Obtém, desse modo, nove
predicados absolutos, que aparecem escritos ao redor de seu quadro: a bondade,
a magnitude, a duração, o poder, a sabedoria, a vontade, a virtude, a verdade,
a magnificência; em seguida, vêm nove predicados relativos: a diferença, a
unanimidade, a contraposição, o princípio, a metade, o fim, o ser maior, o ser
igual e o ser menor; em terceiro lugar, temos as perguntas: sim?, quê?, de
onde?, por quê?, quão grande?, de que qualidade?, quando?, de onde?, como e com
quê?, a última das quais encerra duas determinações; em quarto lugar, aparecem
nove substâncias (esse), a saber: Deus (divinum), os anjos (angelicum), o céu
(coeleste), o homem (humanum), Imaginativum, Sensitivum, Vegetativum,
Elementativum; em quinto lugar, nove acidentes, quer dizer, nove critérios
naturais: a quantidade, a qualidade, a relação, a atividade, a paixão, o ter, a
situação, o tempo e o lugar; por último, nove critérios morais, que são as
virtudes: a justiça, a prudência, a valentia, a temperança, a fé, a esperança,
o amor, a paciência e a piedade, e nove vícios: a inveja, a cólera, a
inconstância, a avareza, a mentira, a gula, a devassidão, o orgulho e a
preguiça (acedia). Todos esses círculos tinham de ser colocados necessariamente
de determinado modo para poder dar como resultado as combinações desejadas.
Conforme as regras de colocação, segundo as quais todas as substâncias recebem
os predicados absolutos e relativos adequados a estes, deviam ser esgotados a
ciência geral, a verdade e o conhecimento de todos os objetos concretos." [Roc81].
Os
procedimentos estabelecidos por Lúlio não foram muito válidos. Mas o mais
importante em Lúlio é a idéia concebida, genial sob certo aspecto. Tanto que seu
trabalho influenciará muitos matemáticos famosos, do nível de um Cardano
(1545), Descartes (1598-1650), Leibniz (1646-1716), Cantor (1829-1920), entre
outros. Raimundo Lúlio é considerado o precursor da análise combinatória. Como
dirá R. Blanché: "encontramos em Lúlio, pelos menos em germe e por mais
que ele não soubesse tirar partido disso por inabilidade, duas idéias que iriam
se tornar predominantes nas obras de Lógica, primeiro em Leibniz e depois em
nossos contemporâneos: as idéias de característica e as idéias de cálculo
(...). Com a ajuda desse simbolismo, eles pretendem permitir que as operações
mentais frequentemente incertas fossem substituídas pela segurança de operações
quase mecânicas, propostas de uma vez por todas"([RA91], volume III).
Pode-se
ver em Raimundo Lúlio os primórdios do desenvolvimento da Lógica Matemática,
isto é, de um novo tratamento da ciência da Lógica: o procurar dar-lhe uma
forma matemática. Não é do interesse deste trabalho aprofundar-se nas
discussões filosóficas - que ainda estão em aberto por sinal - sobre os
conceitos "lógica matemática" e "lógica simbólica", se é
uma lógica distinta da ciência matemática ou não, etc., mas em caracterizá-la,
pois sem dúvida alguma a Computação emergirá dentro de um contexto da evolução
deste novo tratamento da lógica.
A Lógica
Matemática ergue-se a partir de duas idéias metodológicas essencialmente
diferentes. Por um lado é um cálculo, daí sua conexão com a matemática. Por
outro lado, caracteriza-se também pela idéia de uma demonstração exata
e, neste sentido, não é uma imitação da matemática nem esta lhe serve de
modelo, mas pelo contrário, à Lógica caberá investigar os fundamentos da
matemática com métodos precisos e oferecer-lhe o instrumento para uma
demonstração rigorosa.
A
palavra Álgebra voltará a aparecer com o inglês Robert Recorde(1510?-1558), em
sua obra Pathway of Knowledge(1551), que introduz o sinal de '= ' e
divulga os símbolos '+ ' e '- ', introduzidos por John Widmann (Arithmetica,
Leipzig, 1489). Thomas Harriot(1560-1621) prosseguirá o trabalho de Recorde,
inventando os sinais '> ' e '< '. Willian Oughtred(1574-1621), inventor
da régua de cálculo baseada nos logaritmos de Napier, divulgou o uso do sinal
'´ ', tendo introduzido os termos seno, coseno e tangente. Em 1659 J.H.
Rahn usou o sinal '¸ ' . Todos esses matemáticos ajudaram a dar à Álgebra sua
forma mais moderna.
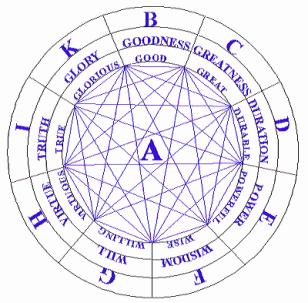
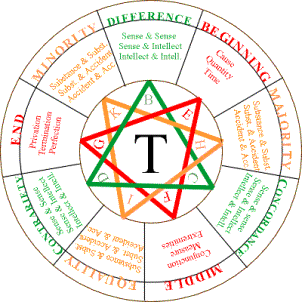
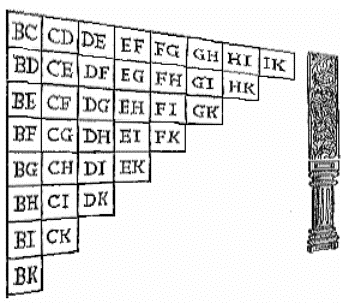
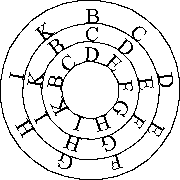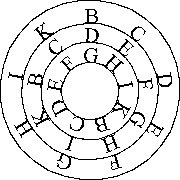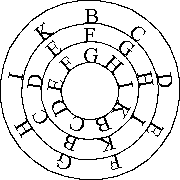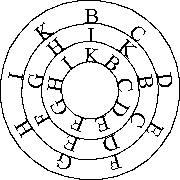
Algumas figuras representando o
dispositivo lógico pensado por Lúlio
Se é
aceito o ponto de vista de estudiosos como Needham [Nee59], a data de 1600 pode ser
vista como um bom divisor de águas dentro da história da ciência em geral. Vale
a pena lembrar que o estudo da matemática no tempo anterior a essa data, na
Europa, não havia avançado substancialmente em relação ao mundo árabe, hindu ou
chinês.
A
álgebra árabe fora perfeitamente dominada e tinha sido aperfeiçoada, e a
trigonometria se tornara uma disciplina independente [Boy74]. O casamento de ambas
pela aplicação dos métodos algébricos no terreno da geometria foi o grande
passo e Galileu (1564 - 1642) aí tem um papel preponderante. Ele uniu o experimental
ao matemático, dando início à ciência moderna. Galileu dá uma contribuição
decisiva a uma formulação matemática das ciências físicas. A partir de então,
em resultado desse encontro da matemática com a física, a ciência tomou um novo
rumo, a um passo mais rápido, e rapidamente as descobertas de Newton (1643
-1727) sucedem às de Galileu.
Trata-se
de um período de transição por excelência, que preparou o caminho para uma nova
matemática: não já uma coleção de truques, como Diophantus possuíra, mas uma
forma de raciocinar, com uma notação clara. É o começo do desenvolvimento da
idéia de formalismo na Matemática, tão importante depois para a fundamentação
teórica da Computação§9 .
Leibniz, o precursor da Lógica Matemática
moderna
A Lógica
Moderna começou no século XVII com o filósofo e matemático alemão Gottfried
Wilhelm Leibniz (1646 - 1716). Seus estudos influenciaram, 200 anos mais tarde,
vários ramos da Lógica Matemática moderna e outras áreas relacionadas, como por
exemplo a Cibernética (Norbert Wiener dizia que "se fosse escolher na
História da Ciência um patrono para a Cibernética, elegeria Leibniz" [Wie70]).
Entre
outras coisas, Leibniz queria dotar a Metafísica (aquela parte da Filosofia que
estuda o "ser" em si) de um instrumento suficientemente poderoso que
a permitisse alcançar o mesmo grau de rigor que tinha alcançado a Matemática.
Parecia-lhe que o problema das interrogações e polêmicas não resolvidas nas
discussões filosóficas, assim como a insegurança dos resultados, eram
fundamentalmente imputáveis à ambigüidade dos termos e dos processos
conclusivos da linguagem ordinária. Leibniz tentaria elaborar sua nova lógica
precisamente como projeto de criação de uma lógica simbólica e de caráter
completamente calculístico, análogos aos procedimentos matemáticos.
Historicamente falando, tal idéia já vinha sendo amadurecida, depois dos
rápidos desenvolvimentos da Matemática nos séculos XVI e XVII, possibilitados
pela introdução do simbolismo. Os algebristas italianos do século XVI já tinham
encontrado a fórmula geral para a resolução das equações de terceiro e quarto
graus, oferecendo à Matemática um método geral que tinha sido exaustivamente
buscado pelos antigos e pelos árabes medievais. Descartes e Fermat criaram a
geometria analítica, e, depois de iniciado por Galileu, o cálculo infinitesimal
desenvolveu-se com grande rapidez, graças a Newton e ao próprio Leibniz. Ou
seja, as matemáticas romperam uma tradição multissecular que as havia encerrado
no âmbito da geometria, e estava se construindo um simbolismo cada vez mais
fácil de manejar e seguro, capaz de funcionar de uma maneira, por assim dizer,
mecânica e automática, sujeito a operações que, no fundo, não eram mais do que
regras para manipulação de símbolos, sem necessidade de fazer uma contínua
referência a conteúdos geométricos intuitivos.
Leibniz
deu-se conta de tudo isto e concebeu, também para a dedução lógica, uma
desvinculação análoga com respeito ao conteúdo semântico das proposições, a
qual além de aliviar o processo de inferência do esforço de manter presente o
significado e as condições de verdade da argumentação, pusesse a dedução a
salvo da fácil influência que sobre ela pode exercer o aspecto material das
proposições. Deste modo coube a Leibniz a descoberta da verdadeira natureza do
"cálculo" em geral, além de aproveitar pela primeira vez a
oportunidade de reduzir as regras da dedução lógica a meras regras de cálculo,
isto é, a regras cuja aplicação possa prescindir da consideração do conteúdo
semântico das expressões.
Leibniz
influenciou seus contemporâneos e sucessores através de seu ambicioso programa
para a Lógica. Este programa visava criar uma linguagem universal baseada em um
alfabeto do pensamento ou characteristica universalis, uma espécie de
cálculo universal para o raciocínio.
Na visão
de Leibniz a linguagem universal deveria ser como a Álgebra ou como uma versão
dos ideogramas chineses: uma coleção de sinais básicos que padronizassem noções
simples não analíticas. Noções mais complexas teriam seu significado através de
construções apropriadas envolvendo sinais básicos, que iriam assim refletir a
estrutura das noções complexas e, na análise final, a realidade. O uso de
numerais para representar noções não analíticas poderia tornar possível que as
verdades de qualquer ciência pudessem ser "calculadas" por operações
aritméticas, desde que formuladas na referida linguagem universal ([Bri79a],
volume XI). Com isso se poderia substituir o genérico
dialoguemos por um mais exato calculemos. Conforme o próprio Leibniz,
"Quando orietur controversiae, non magis disputatione opus erit inter duo
philosophos, quam inter duo computistas. Sufficet enin calamos in manus sumere,
sedereque ad ábacos et sib mutuo (accito si placet amico) dicere:
calculemus"§10
. As discussões não seriam, assim, disputas controvertidas, de resultado
duvidoso e final não concluído, mas sim formas de cálculo que estabelecessem a
maior ou menor verdade de uma proposição.
Essa idéia de Leibniz sustentava-se em dois conceitos intimamente relacionados:
o de um simbolismo universal e o de um cálculo de raciocínio (isto é, um método
quase mecânico de raciocínio) . Isso, para a História da Computação, tem um
particular interesse, pois esse calculus ratiocinator de Leibniz contém o
embrião da machina ratiocinatrix, a máquina de raciocinar buscada por Turing e
depois pelos pesquisadores dentro do campo da Inteligência Artificial. Leibniz,
assim como Boole, Turing, e outros - basta lembrar o ábaco, o 'computador' de
Babbage, etc. -, perceberam a possibilidade da mecanização do cálculo
aritmético. O próprio Leibniz, e Pascal um pouco antes, procuraram construir
uma máquina de calcular. Nota-se portanto que o mesmo impulso intelectual que o
levou ao desenvolvimento da Lógica Matemática o conduziu à busca da mecanização
dos processos de raciocínio.
Interessa também chamar a atenção sobre a idéia de uma linguagem artificial que
já aparece em Leibniz. Como já foi dito, ele captou muito bem as inúmeras
ambigüidades a que estão submetidas as linguagens de comunicação ordinárias e
as vantagens que apresentam os símbolos (que ele chamava notae) da Aritmética e
Álgebra, ciências nas quais a dedução consiste no emprego de caracteres. Ao
querer dar à Lógica uma linguagem livre de ambigüidades e ao procurar associar
a cada idéia um sinal e obter a solução de todos os problemas mediante a
combinação desses sinais, Leibniz acabou provocando um novo desenvolvimento da
própria lógica.
Ainda
dentro desses primeiros passos mais concretos em direção à construção de um
dispositivo para cálculo automático, não se pode deixar de falar do ilustre
francês da imagem ao lado, Blaise Pascal (1623-1662), já acima citado, que foi
matemático, físico, filósofo e brilhante escritor de religião, fundador da
teoria moderna das probabilidades. Aos 17 anos já publicava ensaios de
matemática que impressionaram a comunidade do seu tempo. Antecedendo a Leibniz,
montou a primeira máquina de cálculo digital para ajudar nos negócios do pai em
1642. Iria produzir ainda outras 49 máquinas a partir deste primeiro modelo.
Estudos posteriores em geometria, hidrodinâmica, hidrostática e pressão atmosférica
o levaram a inventar a seringa e prensa hidráulica e descobrir as famosas Leis
de Pressão de Pascal. Após intensa experiência mística, entrou em 1654 para o
convento de Port-Royal, onde escreveu pequenos opúsculos místicos. Os últimos
anos de sua vida foram dedicados à pesquisa científica [Wil97].
Nas
ciências, as descobertas que podem ser compreendidas e assimiladas rapidamente por
outros são fonte de progresso imediato. E na Matemática, o conceito de notação
está relacionado com isso. Basta lembrar os algarismos romanos e pensar na
complexidade que envolve, por exemplo a multiplicação, de MLXXXIV por MMLLLXIX.
Há uma
forte analogia entre a história da Álgebra e a da Aritmética. No caso desta
última, os homens esforçaram-se durante centenas de anos usando uma numeração
inadequada, devido à ausência de um símbolo para o 'nada' (zero). Na Álgebra, a
ausência de uma notação reduziu-a a uma coleção de regras fortuitas para a
solução de equações numéricas. A descoberta do zero criou a Aritmética que é
hoje ensinada e utilizada, e o mesmo se pode dizer em relação à notação, que
acabou por introduzir uma nova etapa na história da Álgebra.
As
letras liberaram a Álgebra da dependência do uso de palavras, sujeitas às
ambigüidades e diferentes interpretações a que está sujeito o discurso de uma
linguagem natural (português, inglês, e outras). Mais ainda: a letra ficou
livre dos tabus que a associavam à palavra. Ela é agora um símbolo cujo
significado pode transcender o objeto simbolizado. O 'x' de uma equação tem
existência própria, independente do objeto que represente.
Importante
também é o fato de se poder operar com letras e transformar expressões
algébricas com literais, mudando um sentença qualquer para diferentes formas
com sentido equivalente. A Álgebra não se torna somente uma maneira mais
econômica de se escrever, mas generaliza procedimentos. Por exemplo: expressões
tais como 2x + 3, 3x - 5, x2 + 4x +7 tinham antes uma individualidade própria,
eram fechadas em si mesmas através das palavras com que eram expressas. Sua
resolução dependia de uma apropriada interpretação e manipulação. Com a notação
através de literais é possível passar de um individual para um coletivo. A
forma linear ax+b, a forma quadrática ax2+bx+c são agora espécies, 'moldes'
específicos, e graças a isso foi possível o nascimento da teoria geral das
funções que é a base de toda matemática aplicada [Dan54].
A notação de Leibniz usada para o cálculo contribuiu mais do que a de Newton
para a difusão das novas idéias sobre integrais§11 , na época. Pense-se por
um momento como se resolve ax = b. Imediatamente pode ser dado como resposta
que x = b/a e haveria surpresa se alguém respondesse a = b/x. É que normalmente
se usam as últimas letras do alfabeto para representar as incógnitas e as do
começo para representar as quantidades conhecidas. Mas isso não foi sempre
assim, e somente no século XVII, a partir de Viète e com Descartes, tais
convenções começaram a ser usadas [Boy74].
Geralmente
tende-se a apreciar o passado desde o sofisticado posto de observação do tempo
atual. É necessário valorizar e revalorizar este difícil e longo passado de
pequenas e grandes descobertas. Leibniz, em seu esforço no sentido de reduzir
as discussões lógicas a uma forma sistemática que pudesse ser universal,
aproximou-se da Lógica Simbólica formal: símbolos ou ideogramas deveriam ser
introduzidos para representar um pequeno número de conceitos fundamentais
necessários ao pensamento. As idéias compostas deveriam ser formadas a partir
desses "alfabetos" do pensamento humano, do mesmo modo como as
fórmulas são desenvolvidas na Matemática [Boy74]. Isso o levou, entre
outras coisas, a pensar em um sistema binário para a Aritmética e a demonstrar
a vantagem de tal sistema sobre o decimal para dispositivos mecânicos de
calcular§12
. A idéia de uma lógica estritamente formal - da construção de sistemas sem
significado smântico, interpretáveis a posteriori - não tinha surgido. Duzentos
anos mais tarde, George Boole formularia as regras básicas de um sistema
simbólico para a lógica matemática, refinado posteriormente por outros
matemáticos e aplicado à teoria dos conjuntos ([Bri79a], volume III). A álgebra
booleana constituiu a base para o projeto de circuitos usados nos computadores
eletrônicos digitais.
A
lógica matemática no século XIX
A
passagem do século XVIII para o século XIX marca o início de um novo tempo na
História da matemática, e, mais do que qualquer período precedente, mereceu ser
conhecido como a sua "Idade áurea", e que afetará diretamente a
evolução em direção ao surgimento e fundamentação da Ciência da Computação. O
que se acrescentou ao corpo da Matemática durante esses cem anos, supera de
longe tanto em quantidade como em qualidade a produção total combinada de todas
as épocas precedentes. Com uma possível exceção do período conhecido como
"Idade heróica", na Grécia antiga, foi uma das mais revolucionárias
etapas do desenvolvimento dessa ciência, e, conseqüentemente, também da
Computação. Será particularmente objeto de estudo a evolução da Lógica
Simbólica - ou Lógica Matemática - que teve Leibniz como predecessor distante.
A partir de meados do século XIX, a lógica formal se elabora como um cálculo
algébrico, adotando um simbolismo peculiar para as diversas operações lógicas.
Graças a esse novo método, puderam-se construir grandes sistemas axiomáticos de
lógica, de maneira parecida com a matemática, com os quais se podem efetuar com
rapidez e simplicidade raciocínios que a mente humana não consegue
espontaneamente.
A Lógica
Simbólica - Lógica Matemática a partir daqui -, tem o mesmo objeto que a lógica
formal§13
tradicional: estudar e fazer explícitas as formas de inferência, deixando de
lado - por abstração - o conteúdo de verdades que estas formas possam
transmitir [San82]. Não se trata
aqui de estudar Lógica, mas de chamar a atenção para a perspectiva que se
estava abrindo com o cálculo simbólico: a automatização de algumas operações do
pensamento. A Máquina de Turing, como será visto, conceito abstrato que
efetivamente deu início à era dos computadores, baseou-se no princípio de que a
simples aplicação de regras permite passar mecanicamente de uns símbolos a
outros, sistema lógico que foi inaugurado pelo matemático George Boole.
Entretanto
a lógica booleana estava limitada ao raciocínio proposicional, e somente mais
tarde, com o desenvolvimento dos quantificadores, a lógica formal estava pronta
para ser aplicada ao raciocínio matemático em geral. Os primeiros sistemas
foram desenvolvidos por F.L.G. Frege e G. Peano. Ao lado destes, será
necessário citar George Cantor (figura, 1829 - 1920), matemático alemão
que abriu um novo campo dentro do mundo da análise, nascida com Newton e
Leibniz, com sua teoria sobre conjuntos infinitos [Bel37].
No
início do século XX a Lógica Simbólica se organizará com mais autonomia em
relação à matemática e se elaborará em sistemas axiomáticos desenvolvidos, que
se colocam em alguns casos como fundamento da própria matemática e que
prepararão o surgimento do computador.
Boole e os fundamentos da Lógica Matemática
e da Computação
O inglês
George Boole (1815 - 1864) é considerado o fundador da Lógica Simbólica ([Bri79a],
volume III). Ele desenvolveu com sucesso o primeiro sistema
formal para raciocínio lógico. Mais ainda, Boole foi o primeiro a enfatizar a
possibilidade de se aplicar o cálculo formal a diferentes situações, e fazer
operações com regras formais, desconsiderando noções primitivas.
Sem
Boole, que era um pobre professor autodidata em Matemática, o caminho pelo qual
se ligou a Lógica à Matemática talvez demorasse muito a ser construído. Com
relação à Computação, se a Máquina Analítica de Babbage (ver capítulo sobre a Pré-História
Tecnológica) foi apenas uma tentativa bem inspirada (que teve pouco efeito
sobre os futuros construtores do computador), sem a álgebra booleana, no
entanto, a tecnologia computacional não teria progredido com facilidade até a
velocidade da eletrônica.
Durante
quase mais de dois mil anos, a lógica formal dos gregos, conhecida pela sua
formulação silogística, foi universalmente considerada como completa e incapaz
de sofrer uma melhora essencial. Mais do que isso, a lógica aristotélica
parecia estar destinada a ficar nas fronteiras da metafísica, já que somente se
tratava, a grosso modo, de uma manipulação de palavras. Não se havia ainda dado
o salto para um simbolismo efetivo, embora Leibniz já tivesse aberto o caminho
com suas idéias sobre o "alfabeto do pensamento"§14 .
Foi
Boole, em sua obra The Mathematical Analysis of Logic (1847), quem forneceu uma
idéia clara de formalismo, desenvolvendo-a de modo exemplar. Ele percebeu que
poderia ser construída uma álgebra de objetos que não fossem números, no
sentido vulgar, e que tal álgebra, sob a forma de um cálculo abstrato, seria
capaz de ter várias interpretações [Kne68].
O que chamou a atenção na obra foi a clara descrição do que seria a essência do
cálculo, isto é, o formalismo, procedimento, conforme descreveu, "cuja
validade não depende da interpretação dos símbolos mas sim da exclusiva
combinação dos mesmos" [Boc66].
Ele concebeu a lógica como uma construção formal à qual se busca posteriormente
uma interpretação.
Boole criou o primeiro sistema bem sucedido para o raciocínio lógico, tendo
sido pioneiro ao enfatizar a possibilidade de se aplicar o cálculo formal em
diferentes situações e fazer cálculos de acordo com regras formais,
desconsiderando as interpretações dos símbolos usados. Através de símbolos e
operações específicas, as proposições lógicas poderiam ser reduzidas a equações
e as equações silogísticas poderiam ser computadas de acordo com as regras da
álgebra ordinária. Pela aplicação de operações matemáticas puras e contando com
o conhecimento da álgebra booleana é possível tirar qualquer conclusão que
esteja contida logicamente em qualquer conjunto de premissas específicas.
De
especial interesse para a Computação, sua idéia de um sistema matemático
baseado em duas quantidades, o 'Universo' e o 'Nada', representados por '1' e
'0', o levou a inventar um sistema de dois estados para a quantificação lógica.
Mais tarde os construtores do primeiro computador entenderam que um sistema com
somente dois valores pode compor mecanismos para perfazer cálculos§15
.
George
Boole estava convencido de que sua álgebra não somente tinha demonstrado a equivalência
entre Matemática e Lógica, como representava a sistematização do pensamento
humano. Na verdade a ciência, depois dele, principalmente com Husserl, pai da
Fenomenologia, demonstrará que a razão humana é mais complicada e ambígua,
difícil de ser conceituada e mais poderosa que a lógica formal, mas do ponto de
vista da Matemática e da Computação, a álgebra booleana foi importante, e só os
anos fizeram ver, pois a lógica até então era incompleta e não explicava muitos
princípios de dedução empregados em raciocínios matemáticos elementares.
Mas, a
lógica booleana estava limitada ao raciocínio proposicional, e somente após o
desenvolvimento de quantificadores, introduzidos por Peirce, é que a lógica
formal pôde ser aplicada ao raciocínio matemático geral. Além de Peirce, também
Schröeder e Jevons§16
aperfeiçoaram e superaram algumas restrições do sistema booleano: disjunção
exclusiva, emprego da letra v para exprimir proposições existenciais, admissão
de coeficientes numéricos além do 0 e 1 e o emprego do sinal de divisão. O
resultado mais importante, no entanto, foi a apresentação do cálculo de uma
forma extremamente axiomatizada.
A importância de Frege e Peano
Frege (1848-1925)
e Peano (1858-1932) trabalharam para fornecer bases mais sólidas à álgebra e
generalizar o raciocínio matemático [Har96].
Gottlob
Frege (imagem) ocupa um lugar de destaque dentro da Lógica. Embora não tão
conhecido em seu tempo e bastante incompreendido, deve-se ressaltar que ainda
hoje torna-se difícil descrever a quantidade de conceitos e inovações, muitas
revolucionárias, que elaborou de forma exemplar pela sua sistematização e
clareza. Muitos autores comparam seu Begriffsschrift aos Primeiros
Analíticos de Aristóteles, pelos pontos de vista totalmente geniais.
Frege
foi o primeiro a formular com precisão a diferença entre variável e constante,
assim como o conceito de função lógica, a idéia de uma função de vários
argumentos, o conceito de quantificador§17. A ele se deve uma conceituação muito mais
exata da teoria aristotélica sobre sistema axiomático, assim como uma clara
distinção entre lei e regra, linguagem e metalinguagem. Ele é autor da teoria
da descrição e quem elaborou sistematicamente o conceito de valor. Mas isto não
é tudo, pois todas estas coisas são apenas produtos de um empreendimento muito
maior e fundamental, que o inspirou desde suas primeiras pesquisas: uma
investigação das características daquilo que o homem diz quando transmite
informação por meio de juízos.
Na
verdade o que Frege chamou de Lógica - assim como seus contemporâneos Russell e
Wittgenstein - não é o que hoje é chamado Lógica, fruto do formalismo e da
teoria dos conjuntos que acabaram por predominar entre os matemáticos, mas sim
nossa semântica, uma disciplina sobre o conteúdo, natureza desse
conteúdo e estrutura. Frege gastou considerável esforço na separação de suas
concepções lógicas daquelas concepções dos 'lógicos computacionais' como Boole,
Jevons e Schröeder. Estes estavam, como já foi dito, empenhados no
desenvolvimento de um cálculo do raciocínio como Leibniz propusera, mas Frege
queria algo mais ambicioso: projetar uma lingua characteristica. Dizia
ele que uma das tarefas da filosofia era romper o domínio da palavra sobre o
espírito humano. O uso de um sistema simbólico, que até então somente se
pensava para a matemática, procurou-o usar Frege também para a filosofia: um
simbolismo que retratasse o que se pode dizer sobre as coisas. Ele buscava algo
que não somente descrevesse ou fosse referido a coisas pensadas, mas o próprio
pensar[Cof91].
Os
lógicos tradicionais estavam basicamente interessados na solução de problemas
tradicionais de lógica, como por exemplo a validade. O objetivo de Frege foi
mais além: entrou no campo da semântica, do conteúdo, do significado, onde
encontrou o fundamento último da inferência, da validade, etc. Frege acabou
derivando para uma filosofia da lógica e da matemática e influenciou
diretamente a Russell, David Hilbert, Alonzo Church e Carnap. Destes, Hilbert e
Church têm um papel decisivo na História conceitual da Ciência da Computação.
Frege
desejava provar que não somente o raciocínio usado na matemática, mas também os
princípios subjacentes - ou seja, toda a matemática - são pura lógica. Porém
ele expressou suas buscas e resultados - pelos quais acabou sendo considerado
um dos pais da Lógica moderna, de uma forma excessivamente filosófica, em uma
notação matemática não convencional. O mérito maior de Frege foi elaborar uma
concepção lógica mais abrangente do que a Lógica de Aristóteles. Em um
procedimento que lembra a "characteristica universalis"§18, Frege construiu
um sistema especial de símbolos para desenvolver a lógica de maneira exata e
foi muito além das proposições e dos argumentos. Em sua grandes obras, Begriffsschrift
(Ideografia ou Conceitografia) e Grundgesitze (Leis Fundamentais da
Aritmética, Ideograficamente Deduzidas), está contida de modo explícito e
plenamente caracterizado uma série de conceitos - conectivos, função, função
proposicional, quantificadores, etc. - que seriam vitais para a Lógica
Matemática a partir de então[Gom97].
Foi
através do contato com a obra de Frege que Bertrand Russell procurou levar
avante a idéia de construir toda a matemática sobre bases lógicas, convencido
de que ambas são idênticas. Os postulados fregianos§19, adotados
primeiramente por Peano, foram incorporados por Russell, que extendeu as teses
logicistas de Frege à Geometria e às disciplinas matemáticas em geral.
Peano
(imagem) tinha objetivo semelhante a Frege, mas mais realista. Ele desenvolveu
uma notação formal para raciocínio matemático que procurasse conter não só a
lógica matemática mas todos os ramos mais importantes dela. O simbolismo de
Peano e seus axiomas - dos quais dependem tantas construções rigorosas na
álgebra e análise - "representam a mais notável tentativa do século de
reduzir a aritmética comum, e portanto a maior parte da matemática, a um puro
simbolismo formal. Aqui o método postulacional atingiu novo nível de precisão,
sem ambiguidade de sentido, sem hipóteses ocultas"[Boy74].
Já
Hilbert procurou colocar em prática a teoria da demonstração de Frege, e
pode-se ver nessas palavras de Frege as idéias implementadas posteriormente no
programa hilbertiano: "a inferência procede pois, em meu sistema de
escrita conceitual (Begriffsschrift), seguindo uma espécie de cálculo. Não me
refiro a este em sentido estrito, como se fosse um algoritmo que nele
predominasse, (...), mas no sentido de que existe um algoritmo total, quer
dizer, um conjunto de regras que resolvem a passagem de uma proposição ou de
duas, a outra nova, de tal forma que nada se dá que não esteja de acordo com
estas regras. Minha meta é pois uma ininterrupta exigência de precisão no
processo de demonstração, e a máxima exatidão lógica, ao mesmo tempo que
clareza e brevidade"[Boc66].
Pode-se notar
a partir desse momento uma guinada no conceito de Lógica: o objeto da
investigação lógica já não são mais as próprias fórmulas, mas as regras de
operação pelas quais se formam e se deduzem.
O desenvolvimento da Lógica Matemática
Uma das
metas dos matemáticos no final do século XIX foi a de obter um rigor conceitual das noções do cálculo
infinitesimal (limite, continuidade, infinito matemático, etc.). Tal programa
foi chamado de “aritmetização da análise”, isto é, a busca da redução dos
conceitos fundamentais da análise (a matemática que tem como base a teoria dos
número reais) aos conceitos da aritmética (a matemática que tem como base a
teoria dos número inteiros positivos, isto é, dos números naturais e, por
extensão, dos números racionais).
Por
exemplo, ao invés de se tomar o número imaginário 
como uma
entidade um tanto misteriosa, pode-se defini-lo como um par ordenado de números
inteiros (0,1), sobre o qual se realizam certas operações de “adição” e
“multiplicação”. Analogamente, o número irracional 
se definia numa
certa classe de números irracionais, cujo quadrado é menor do que 2. Dado que a
Geometria podia ser reduzida à Análise (Geometria Analítica), a Aritmética
vinha a se configurar como a base natural de todo o edifício matemático. O
ponto culminante deste processo foram os axiomas de Peano (1899), que
fundamentaram toda a Aritmética elementar posterior.
Ao mesmo tempo, matemáticos como Frege, Cantor e
Russell, não convencidos da “naturalidade” da base constituída pela aritmética,
procuravam conduzir a própria aritmética a uma base mais profunda, reduzindo o
conceito de número natural ao conceito lógico de classe, ou para recorrer a
Cantor, definir número em termos de conjunto, de modo que a lógica das classes
apresentava-se como a teoria mais adequada para a investigação sobre os
fundamentos da matemática. O esforço dos matemáticos foi o de dar à álgebra uma estrutura lógica, procurando
caracterizar a matemática não tanto pelo seu conteúdo quanto pela sua forma.
Bochenski
[Boc66],
falando da história da Lógica Matemática, diz que a partir de 1904, com
Hilbert, inicia-se um novo período dessa ciência então emergente, que se
caracteriza pela aparição da Metalógica§20 (Hilbert,
Löwenheim e Scholem) e, a partir de 1930, por uma sistematização formalista
dessa mesma Metalógica. Iniciaram-se discussões sobre o valor e os limites da
axiomatização, o nexo entre Lógica e Matemática, o problema da verdade
(Hilbert, Gödel, Tarski).
A
Metalógica, em sua vertente sintática
ocupa-se das propriedades externas dos cálculos, como por exemplo a consistência,
a completude, a decidibilidade dos sistemas axiomáticos e a independência dos
axiomas. Hilbert, Gödel e Church são autores nesse campo. Em sua parte semântica, a Metalógica dirige-se ao
significado dos símbolos, dos cálculos com relação a um determinado mundo de
objetos. Tarski, Carnap e Quino, entre outros se interessaram por estas
questões.
Apareceram
também novos sistemas lógicos: as lógicas
naturais, de Gentzen e Jaskowski, lógica
polivalente de Post e Lukasiewicz, e a lógica intuicionista de Heytings.
Complementando
essas idéias cabe destacar alguns sistemas originais de outros matemáticos como
Schönfinkel (1924), Curry (1930), Kleene (1934), Rosser (1935) e o já citado
Alonzo Church (1941). Deve-se lembrar que quase todos estes últimos, junto com
o logicista inglês Alan M. Turing, acabaram por definir, antes mesmo de existir
o computador propriamente, a natureza da computação, e as implicações e limites
do pensamento humano através de uma máquina.
A crise dos fundamentos e as tentativas de superação
Os matemáticos são conhecidos por serem exigentes
na hora de pedir uma prova absoluta antes de aceitarem qualquer afirmação. Esta
reputação é claramente mostrada em uma anedota:
Um astrônomo, um físico e um matemático estavam passando férias na
Escócia. Olhando pela janela do trem eles avistaram uma ovelha preta no meio de
um campo. “Que interessante”, observou o astrônomo, “na Escócia todas as
ovelhas são pretas.” Ao que o físico respondeu: “Não, nada disso!. Algumas
ovelhas escocesas são pretas.” O matemático olhou para cima em desespero e
disse: “Na Escócia existe pelo menos um campo, contendo pelo menos uma ovelha e
pelo menos um lado dela é preto.”
(Ian Stuart, Conceitos de matemática moderna, in [Sin99])
E o
matemático que se especializa no estudo da lógica matemática é ainda mais
rigoroso do que o matemático comum. Os matemáticos lógicos começaram a
questionar idéias que os outros matemáticos consideravam certas há séculos. Por
exempo, a lei da tricotomia declara
que cada número é ou negativo, ou positivo ou então zero. Ninguém se preocupara
em provar isso que parece óbvio, mas os lógicos perceberam que se não o fosse,
ela poderia ser falsa, e todo o edifício matemático que dependia dessa lei
desmoronaria§21. Apesar das
disciplinas dedutivas terem atingido um alto grau de perfeição lógica, algumas
dúvidas começaram a abalar a confiança dos matemáticos: o surgimento, por volta
de 1900, de inúmeros paradoxos ou antinomias, especialmente na teoria dos
conjuntos§22. O
aparecimento de tais contradições mostrava que havia algum defeito nos métodos.
Será que se poderia ter certeza de que em se usando os axiomas de um sistema
rigidamente lógico – o grande sonho de tantos matemáticos do início do século
XX de reduzir a matemática e o conhecimento à lógica –, nunca se chegaria a uma
contradição, dentro dos axiomas do sistema? Estava iminente, nos fins do século
XIX, uma inevitável colisão entre matemática e filosofia. Alguns vagos
conceitos metafísicos associados com o pensamento humano já tinham chamado a
atenção de matemáticos das duas primeira décadas do século XX§23, que
passaram a procurar a verdadeira natureza do raciocínio dentro da ciência
matemática. O que é um procedimento correto?, qual a relação entre verdade e
demonstração?, é possível fornecer uma prova para todos os enunciados
matemáticos verdadeiros? E o problema das ambigüidades, já que a matemática
sempre foi feita através de uma linguagem natural?
Desde os
antigos gregos a matemática vem acumulando mais teoremas e verdades, e, embora
a maioria deles tenha sido rigorosamente provada, os matemáticos temiam que
alguns casos tivessem sido aceitos sem um exame mais adequado. Os lógicos então
decidiram provar todos os teoremas, a partir de princípios fundamentais. No
entanto, cada verdade tinha sido deduzida de outras verdades. E estas, por sua
vez, de outras ainda mais fundamentais e assim por diante. Acabaram os lógicos
por chegar nos axiomas da matemática, essas declarações essenciais tão
fundamentais que não podiam ser provadas, pois são auto-evidentes§24. O desafio para
os lógicos era reconstruir toda a matemática a partir desses axiomas.
Uma
legião de lógicos participou deste processo, lento e doloroso, usando somente
um número mínimo de axiomas. A idéia era consolidar, através do raciocínio
lógico e rigoroso, o que já se pensava ser conhecido. Este quadro estimulou a
criatividade matemática. Na tentativa de se resolverem os paradoxos surgiram
três grandes escolas da lógica : a Logicista§25, a
Intuicionista§26 e a
Formalista.
A escola
logicista rapidamente ficou exposta a fortes críticas§27. Frege,
Peano e Russell , devido ao seu platonismo, acreditavam em um mundo objetivo,
existente por si mesmo, de entes e relações matemáticas que o pesquisador deve
descobrir e não inventar. Bertrand Russell tinha objetivos ainda maiores:
utilizar o instrumental da lógica como ponto de partida do pensamento
filosófico, através da geração de uma linguagem perfeita. Mas a matemática,
enquanto perquirição pura, independe teoricamente dessas aplicações, bastando
ver as pesquisas atuais. Deve-se, no entanto, destacar o mérito dessa escola de
incrementar grandemente o progresso da logística e confirmar a união íntima
entre matemática e lógica.
O programa intuicionista sofreu também fortes
críticas, principalmente a de desfigurar a matemática, tornando-a algo
subjetivo e praticamente impossível. O próprio modo de se provar a
não-contradição de uma teoria matemática, buscando um ‘modelo’ dos axiomas
dessa teoria dentro de outra teoria já existente (e que era considerada
coerente§28) mostrou-se
pouco confiável: como dar a certeza da não-contraditoriedade dessa outra
teoria? A maior parte dos matemáticos dos nossos dias afastou-se dessa linha de
pensamento. Positivamente falando, sua dura crítica à matemática tradicional
obrigou os especialistas nos fundamentos a desenvolverem novos métodos para
reabilitar a teoria clássica. A escola formalista progrediu bastante através
das polêmicas com os intuicionistas [Cos77].
Para
David Hilbert (1862 - 1943) e outros, o problema de estabelecer fundamentos
rigorosos era o grande desafio ao empreendimento de tantos, que pretendiam
reduzir todas as leis científicas a equações matemáticas. Ele acreditava que
tudo na matemática poderia e deveria ser provado a partir dos axiomas básicos.
O resultado disso levaria a demonstrar conclusivamente, segundo ele, os dois
elementos mais importantes do sistema matemático. Em primeiro lugar a
matemática deveria, pelo menos em teoria, ser capaz de responder a cada
pergunta individual – este é o mesmo espírito de completude que no passado
exigira a invenção de números novos, como os negativos e os imaginários. Em
segundo lugar, deveria ficar livre de inconsistências – ou seja, tendo-se
mostrado que uma declaração é verdadeira por um método, não deveria ser
possível mostrar que ela é falsa por outro método. Hilbert estava convencido de
que, tomando apenas alguns axiomas, seria possível responder a qualquer
pergunta matemática imaginária, sem medo de contradição. O esforço para
reconstruir logicamente o conhecimento matemático acabou sendo liderado por
essa figura, talvez a mais
eminente da época.
No dia 8
de agosto de 1900, Hilbert deu uma palestra histórica no Congresso
Internacional de Matemática em Paris. Ele apresentou vinte e três problemas
não-resolvidos da matemática que acreditava serem de imediata importância.
Alguns problemas relacionavam-se com áreas mais gerais da matemática, mas a
maioria deles estava ligada aos fundamentos lógicos dessa ciência. Tais
problemas deveriam focalizar a atenção do mundo matemático e fornecer um programa
de pesquisas. Hilbert queria unir a comunidade para ajudá-lo a realizar sua
visão de um sistema matemático livre de dúvidas ou inconsistências[Sin99]. Todos esses estudos
denominaram-se Metamatemática ou Metalógica, pela conectividade das duas.
Ele se
propôs demonstrar a coerência da aritmética§29, para
depois estender tal coerência aos âmbitos dos demais sistemas. Apostou na possibilidade
da criação de uma linguagem puramente sintática, sem significado, a partir da
qual se poderia falar a respeito da verdade ou falsidade dos enunciados. Tal
linguagem foi e é chamada de sistema formal, e está resumida no anexo A
concepção formalista da matemática. Isto, que fazia parte do
centro da doutrina formalista, mais tarde estimularia Turing a fazer
descobertas importantes sobre as capacidades das máquinas. Registre-se também
que John von Neumann, a quem muitos atribuem a construção do primeiro
computador, era um aluno de Hilbert e um dos principais teóricos da escola
formalista§30.
Interessam
agora dois problemas da referida lista de vinte e três. O segundo, relacionado
com a confiabilidade do raciocínio matemático (isto é, se ao seguir as regras
de determinado raciocínio matemático não se chegaria a contradições), e, ligado
a ele, o problema de número dez. Este era de enunciado bastante simples:
descreva um algoritmo que determine se uma dada equação diofantina do tipo
P(u1,u2,...,un) = 0, onde P é um polinômio com coeficientes inteiros, tem
solução dentro do conjunto dos inteiros. É o famoso problema da decidibilidade,
o Entscheidungsproblem. Consistia em indagar se existe um procedimento mecânico
efetivo para determinar se todos os enunciados matemáticos verdadeiros poderiam
ser ou não provados, isto é, se eles poderiam ser deduzidos a partir de um dado
conjunto de premissas§31.
Também a
questão da consistência, como já foi dito, era decisiva para ele, pois é uma
condição necessária para o sistema axiomático do tipo que ele tinha em mente.
Aristóteles já tinha mostrado que se um sistema é inconsistente, qualquer
afirmação poderia ser provada como falsa ou verdadeira. Neste caso não seria
possível haver um fundamento sólido para qualquer tipo de conhecimento,
matemático ou não. Anos mais tarde, em 1928, no Congresso Internacional de
Matemáticos, realizado em Bolonha, Itália, Hilbert lançou um novo desafio, que
na verdade somente enfatizava aspectos do segundo e do décimo problema já
descritos. Hilbert queria saber se é possível provar toda assertiva matemática
verdadeira. Estava buscando algo como uma “máquina de gerar enunciados
matemáticos verdadeiros”: uma vez alimentada com um enunciado matemático,
poderia dizer se o enunciado é falso ou verdadeiro [Cas97]. É um problema que está
relacionado com o citado projeto hilbertiano da busca de um sistema formal
completo e consistente.
Ao mesmo
tempo, em 1927, com 22 anos, von Neumann publicou 5 artigos que atingiram
fortemente o mundo acadêmico. Três deles consistiam em críticas à física
quântica, um outro estabelecia um novo campo de pesquisas chamado Teoria dos
Jogos, e, finalmente, o que mais impactou o desenvolvimento da Computação: era
o estudo do relacionamento entre sistemas formais lógicos e os limites da
matemática. Von Neumann demonstrou a necessidade de se provar a consistência da
matemática, um passo importante e crítico tendo em vista o estabelecimento das
bases teóricas da Computação (embora ninguém tivesse esse horizonte por
enquanto).
Já foi
citado, no capítulo sobre o Desenvolvimento da Lógica Matemática, o desafio dos
matemáticos do início do século de aritmetizar a análise. Eles estavam de
acordo, no que diz respeito às proposições geométricas e outros tipos de
afirmações matemáticas, em que poderiam ser reformuladas e reduzidas a
afirmações sobre números. Logo, o problema da consistência da matemática estava
reduzido à determinação da consistência da aritmética. Hilbert estava
interessado em dar uma teoria da aritmética, isto é, um sistema formal que
fosse finitisticamente descritível§32,
consistente, completo e suficientemente poderoso para descrever todas as
afirmações que possam ser feitas sobre números naturais. O que Hilbert queria
em 1928 era que para uma determinada afirmação matemática, por exemplo, “a soma de dois números ímpares é
sempre um número par”, houvesse um procedimento que, após um número finito de
passos, parasse e indicasse se aquela afirmação poderia ou não ser provada em
determinado sistema formal, suficientemente poderoso para abranger a aritmética
ordinária [Cas97]. Isto está
diretamente relacionado com o trabalho de Gödel e Alan Turing.
Pode-se
afirmar que em geral a lógica matemática prestou naqueles tempos maior atenção
à linguagem científica, já que seu projeto era o da elaboração de uma linguagem
lógica de grande precisão, que fosse boa para tornar transparentes as
estruturas lógicas de teorias científicas. Tal projeto encontrou seus limites,
tanto na ordem sintática como na ordem semântica (por exemplo com os célebres
teoremas de limitação formal). Este fenômeno levou a uma maior valorização da
linguagem ordinária, que, apesar de suas flutuações e imprecisões, encerram uma
riqueza lógica que os cálculos formais não conseguem recolher de todo. Dentro
da própria matemática – como se verá mais adiante com Gödel – há verdades que
não podem ser demonstradas mediante uma dedução formal, mas que podem ser
demonstradas – o teorema da incompletude de Gödel é uma prova disso – mediante
um raciocínio metamatemático informal. A partir desse propósito de construção
de uma linguagem ideal surgiu a filosofia da linguagem (Moore, Wittgenstein,
Geach em sua segunda etapa) colocando as questões lógicas sobre nova ótica [San82].
Na
verdade, tanto a lógica matemática em sentido estrito como os estudos de
semântica e filosofia da linguagem depararam-se com problemas filosóficos que
não se resolvem somente dentro de uma perspectiva lógica. Há questões de fundo
da lógica matemática que pertencem já a uma filosofia da matemática.
Todos
esses desafios abriram uma porta lateral para a Computação e deram origem a um
novo e decisivo capítulo na sua História. Da tentativa de resolvê-los ocorreu
uma profunda revolução conceitual na Matemática – o Teorema de Gödel – e surgiu
o fundamento básico de todo o estudo e desenvolvimento da Computação posterior:
a Máquina de Turing.
Kurt Gödel: muito além da lógica
Kurt
Gödel (1906 - 1978) nasceu na Morávia, então parte do império austro-húngaro e
agora parte da república checa. Ainda criança mostrou ter talento para a
ciência e metamática, e sua natureza curiosa levou a família a apelidá-lo der
Herr Warum (senhor por que). Ele foi para a Universidade de Viena sem ter
certeza se devia se especializar em matemática ou física, mas uma aula
inspirada sobre a teoria dos números dada pelo prof. P. Furtwängler persuadiu
Gödel a dedicar sua vida aos números.
Quando
tinha pouco mais de vinte anos, Gödel já se estabelecera no departamento de
matemática, onde gostava de participar, junto com seus colegas, dos encontros
do Wiener Kreis (Círculo Vienense), formado por um grupo de filósofos que se
reunia para discutir as grandes questões da lógica. Foi durante este período
que ele desenvolveu as idéias que abalariam os fundamentos da Matemática.
Em 1931
publicou seu livro Über formal unentscheidbare Sätze der Principia Mathematica
und verwandter Systeme (Sobre as proposições indecidíveis no Principia
Mathematica e Sistemas Relacionados), que continha os chamados teoremas da
indecidibilidade§33.
Suas
idéias podem ser resumidas em duas declarações [Gom97]:
Se S é
um sistema formal suficientemente forte para conter a aritmética elementar,
então S é incompleto ou inconsistente;
A
eventual consistência de um tal sistema formal não pode ser provada apenas com
recursos daquele mesmo sistema.
Essencialmente,
a primeira parte da declaração significa que existem proposições aritméticas
tais que, nem elas nem sua negação, são demonstráveis na aritmética adotada.
São proposições indecidíveis, isto é, não importa o conjunto de axiomas que
está sendo usado, existem problemas que os matemáticos não podem resolver. Pior
ainda, a segunda parte diz que a prova de ausência de contradição em uma
axiomática da aritmética não pode ser realizada apenas com os recursos dessa
axiomática. Ou seja, os matemáticos nunca poderão ter certeza de que sua
escolha de axiomas não os levará a uma contradição. Kurt Gödel demonstrou que
não é possível construir uma teoria axiomática dos números que seja completa,
como pretendia Hilbert.
Para o
desenvolvimento de seus estudos Gödel concebeu uma interessante formulação de
símbolos, fórmulas e provas através de números, bem como mostrou que as
proposições metamatemáticas – aliás sem isso não poderia ter realizado sua
prova – podem estar adequadamente refletidas dentro do próprio cálculo,
aritmetizando assim a própria metamatemática. No anexo O Teorema de
Gödel há um pequeno resumo sobre a prova de Gödel.
Gödel
acabou com o sonho logicista, visto que não se pode desenvolver toda a
aritmética (e muito menos toda a matemática) num sistema que seja ao mesmo
tempo consistente e completo. Também acabou com o sonho formalista: existem
enunciados matemáticos que são verdadeiros, mas não são suscetíveis de prova,
isto é, existe um abismo entre verdade e demonstração§34.
Gödel,
no entanto, ao longo da demonstração do seu teorema, rompeu um limiar crucial
entre a lógica e a matemática. Ele mostrou que qualquer sistema formal que seja
tão rico quanto um sistema numérico qualquer, que contenha os operadores “+” e
“=”, pode ser expresso em termos aritméticos [Coh87]. Isto significa que por
mais complexa que se torne a matemática (ou qualquer outro sistema formal
redutível a ela), ela pode sempre ser expressa em termos de operações a serem
executadas sobre números, e as partes do sistema poderão ser manipuladas por
regras de contagem e comparação. Outro resultado fundamental do teorema da
incompletude de Gödel pode-se considerar como sendo a demonstração de que há
algumas funções sobre os inteiros que não podem ser representadas por um
algoritmo, ou seja, que não podem ser computadas§35.
Posteriormente verificou-se a existência de uma equivalência entre o Teorema da
Incompletude de Gödel e o problema da parada de Turing.
Alan Mathison Turing: o berço da Computação
A
revolução do computador começou efetivamente a realizar-se no ano de 1935, em
uma tarde de verão na Inglaterra, quando Alan M. Turing (1912-1954), estudante do
King's College, Cambridge, durante curso ministrado pelo matemático Max
Neumann, tomou conhecimento do Entscheidungsproblem de Hilbert. Enquanto isso,
conforme foi brevemente citado no item precedente, uma parte da comunidade dos
matemáticos buscava um novo tipo de cálculo lógico, que pudesse, entre outras
coisas, colocar em uma base matemática segura o conceito heurístico do que seja
proceder a um cômputo. O resultado destas pesquisas era fundamental para o
desenvolvimento da matemática: tratava-se de saber se é possível haver um
procedimento efetivo para se solucionar todos os problemas de uma determinada
classe que estivesse bem definida. O conjunto desses esforços acabou por formar
a fundamentação teórica da que veio a ser chamada "Ciência da Computação".
Os
resultados de Gödel e o problema da decisão motivaram Turing primeiramente a
tentar caracterizar exatamente quais funções são capazes de ser computadas. Em
1936, Turing consagrou-se como um dos maiores matemáticos do seu tempo, quando
fez antever aos seus colegas que é possível executar operações computacionais
sobre a teoria dos números por meio de uma máquina que tenha embutida as regras
de um sistema formal. Turing definiu uma máquina teórica que se tornou um
conceito chave dentro da Teoria da Computação. Ele enfatizou desde o início que
tais mecanismos podiam ser construídos e sua descoberta acabou abrindo uma nova
perspectiva para o esforço de formalizar a matemática, e, ao mesmo tempo,
marcou fortemente a História da Computação.
A
percepção genial de Turing foi a substituição da noção intuitiva de
procedimento efetivo por uma idéia formal, matemática. O resultado foi a
construção de uma conceituação matemática da noção de algoritmo§36,
uma noção que ele modelou baseando-se nos passos que um ser humano dá quando
executa um determinado cálculo ou cômputo. Turing formalizou definitivamente o
conceito de algoritmo.
Um dos
primeiros modelos de máquina abstrata foi a Máquina de Turing. Conforme o
próprio Turing escreveu: “Computar é normalmente escrever símbolos em um papel.
Suponha que o papel é quadriculado, podendo ser ignorada a bidimensionalidade,
que não é essencial. Suponha que o número de símbolos é finito. [...]. O
comportamento do(a) computador(a)
é determinado pelos símbolos que ele(a) observa num dado momento, e seu estado
mental nesse momento. Suponha que exista um número máximo de símbolos ou
quadrículas que ele(a) possa observar a cada momento. Para observar mais serão
necessárias operações sucessivas. Admitamos um número finito de estados mentais
[...]. Vamos imaginar que as ações feitas pelo(a) computador(a) serão divididas
em operações tão elementares que são indivisíveis. Cada ação consiste na
mudança do sistema computador(a) e papel. O estado do sistema é dado pelos
símbolos no papel, os símbolos observados pelo(a) computador(a) e seu estado
mental. A cada operação, não mais de um símbolo é alterado, e apenas os
observados são alterados. Além de mudar símbolos, as operações devem mudar o
foco da observação, e é razoável que esta mudança deva ser feita para símbolos
localizados a uma distância fixa dos anteriores. [...] Algumas destas operações
implicam mudanças de estado mental do computador(a) e portanto determinam qual
será a próxima ação”.
O
trabalho de Turing ficou documentado no artigo On Computable Numbers with an aplication to the
Entscheidungsproblem, publicado em 1936§37 ([Tur50], volume XII). Ele descreveu em termos
matematicamente precisos como pode ser poderoso um sistema formal automático,
com regras muito simples de operação.
Turing
definiu que os cálculos mentais consistem em operações para transformar números
em uma série de estados intermediários que progridem de um para outro de acordo
com um conjunto fixo de regras, até que uma resposta seja encontrada. Algumas
vezes usam-se o papel e lápis para não se perder o estado dos nossos cálculos.
As regras da matemática exigem definições mais rígidas que aquelas descritas
nas discussões metafísicas sobre os estados da mente humana, e ele
concentrou-se na definição desses estados de tal maneira que fossem claros e
sem ambigüidades, para que tais definições pudessem ser usadas para comandar as
operações da máquina. Turing começou com uma descrição precisa de um sistema
formal, na forma de “tabela de instruções” que especificaria os movimentos a
serem feitos para qualquer configuração possível dos estados no sistema. Provou
então que os passos de um sistema axiomático formal semelhante à lógica e os
estados da máquina que perfaz os “movimentos” em um sistema formal automático
são equivalentes entre si. Estes conceitos estão todos subjacentes na
tecnologia atual dos computadores digitais, cuja construção tornou-se possível
uma década depois da publicação do matemático inglês.
Um
sistema formal automático é um dispositivo físico que manipula automaticamente
os símbolos de um sistema formal de acordo com as suas regras. A máquina
teórica de Turing estabelece tanto um exemplo da sua teoria da computação
quanto uma prova de que certos tipos de máquinas computacionais poderiam ser
construídas. Efetivamente, uma Máquina de Turing Universal§38,
exceto pela velocidade, que depende do hardware, pode emular qualquer
computador atual, desde os supercomputadores até os computadores pessoais, com
suas complexas estruturas e poderosas capacidades computacionais, desde que não
importasse o tempo gasto. Ele
provou que para qualquer sistema formal existe uma Máquina de Turing que
pode ser programada para imitá-lo. Ou em outras palavras: para qualquer
procedimento computacional bem definido, uma Máquina de Turing Universal é
capaz de simular um processo mecânico que execute tais procedimentos.
De um
ponto de vista teórico, a importância da Máquina de Turing está no fato de que
ela representa um objeto matemático formal. Através dela, pela primeira vez, se
deu uma boa definição do que significa computar algo. E isso levanta a questão
sobre o que exatamente pode ser computado com tal dispositivo matemático,
assunto fora do escopo do presente trabalho e que entra no campo da complexidade
computacional.
O problema da parada e o problema da decisão
Turing mostrou que o funcionamento de sua máquina (usar-se-á a sigla MT a
partir de agora) e a aplicação das regras de formação de um sistema formal não têm
diferença. Ele demonstrou também que seu dispositivo poderia resolver infinitos
problemas mas havia alguns que não seriam possíveis, porque não haveria jeito
de se prever se o dispositivo pararia ou não. Colocando de uma outra maneira:
dado um programa P para uma MT e uma determinada entrada de dados E, existe
algum programa que leia P e E, e pare após um número finito de passos, gerando
uma configuração final na fita que informe se o programa P encerra sua execução
após um número finito de passos ao processar E?
Comparando-se
com as afirmações sobre verdades aritméticas, dentro de um sistema formal
consistente da aritmética, que não são passíveis de prova dentro deste sistema,
percebe-se que o problema da parada de Turing nada mais é do que o Teorema de
Gödel, mas expresso em termos de uma máquina computacional e programas ao invés
de uma linguagem de um sistema dedutivo da Lógica Matemática.
Em 1936
Turing provou formalmente o seguinte teorema:
Teorema
da Parada: Dado um programa P qualquer para uma Máquina de Turing e uma entrada
E qualquer de dados para esse programa, não existe uma Máquina de Turing
específica que pare após um número finito de passos, e que diga se P em algum
momento encerra sua execução ao processar E.
A
solução negativa desse problema computacional implica também numa solução
negativa para o problema de Hilbert. Portanto nem todos os enunciados
verdadeiros da aritmética podem ser provados por um computador§39.
A tese de Church-Turing e outros resultados teóricos
Até aqui
foi mostrado como, do ponto de vista formal, surgiu a idéia de computação. Dentro
dessa dimensão formal se procurará mostrar agora que o cume atingido, e ainda
não ultrapassado, foi a Máquina de Turing, esse genial modelo abstrato de
equipamento, com capacidade de processar complicadas linguagens e calcular o
valor de funções aritméticas não-triviais, que pode inclusive ser aperfeiçoada
para realizar operações mais complexas, embora em relação ao modelo básico isto
não implique um salto qualitativo, isto é, que o torne algo mais poderoso.
Em
termos computacionais pode-se dizer que as Máquinas de Turing são um modelo
exato e formal da noção intuitiva de algoritmo: nada pode ser considerado um
algoritmo se não puder ser manipulado por uma Máquina de Turing. O princípio de
que as Máquinas de Turing são versões formais de algoritmos e de que
procedimento computacional algum seja considerado um algoritmo a não ser que
possa ser instanciado por uma Máquina de Turing é conhecido como a Tese de
Church, em homenagem ao brilhante matemático americano Alonzo Church (1903 -
1995), ou ainda Tese de Church-Turing. É uma proposição, não um teorema, porque
não é um resultado matemático: simplesmente diz que um conceito informal
corresponde a um objeto matemático§40.
Fazendo
uma pequena retrospectiva, após os resultados de Gödel em 1931 muitos lógicos
matemáticos partiram em busca do que seria uma noção formalizada de um
procedimento efetivo (por efetivo entenda-se mecânico), ou seja, o que pode ser
feito seguindo-se diretamente um algoritmo ou conjunto de regras (como já
visto, antigo sonho de séculos, que remonta a Leibniz). Destas buscas surgiram:
§
a sistematização e desenvolvimento das funções recursivas (introduzidas nos
trabalhos de Gödel e Herbrand) por
Stephen Cole Kleene (1909-1994) em sua teoria lógica da computabilidade
(parte de seu livro Introdução à Metamatemática, um dos cumes da lógica
matemática dos últimos anos);
§
as Máquinas de Turing;
§
o cálculo-lambda (componente característico fundamental da
linguagem de programação LISP) de Alonzo Church;
§
a Máquina de Post, análoga à de Turing, tornada pública um
pouco depois, fruto de trabalho independente, e seu sistema para rescrita de
símbolos (cuja gramática de Chomsky é um caso particular), de Emil L. Post
(1897 - 1954).
Com
efeito, todos esses conceitos levaram à mesma conclusão e acabaram por ter o
mesmo significado, dentro do citado escopo da busca de uma definição bem
elaborada de processo efetivo. O que
se desenvolverá aqui refere-se mais a Church e Turing (Kleene fez em seu
trabalho uma ampla abordagem de ambos, tirando várias conseqüências, e Post
trata do mesmo tema de Turing), para se ter uma visão mais clara da
diversificação dos estudos da década de 1930, com vistas à fundamentação
teórica de toda a Computação.
Em seu
célebre teorema, Church demonstrou, em 1936, que não pode existir um
procedimento geral de decisão para todas as expressões do Cálculo de Predicados
de 1a ordem, ainda que exista tal procedimento para classes especiais de
expressões de tal cálculo. Isso pode causar certo espanto quando se observa que
o Cálculo de Predicados de 1a ordem é semanticamente completo, com o que se
diz, implicitamente, que o próprio cálculo, com seus axiomas e regras,
constitui um algoritmo capaz de enumerar uma após outra todas as suas
expressões válidas. Estas expressões são em quantidade indefinida, e mesmo
sendo enumeráveis (isto é, elaboráveis passo a passo a partir dos axiomas),
essa enumeração não tem fim. Compreende-se então, que ao se conseguir
demonstrar uma determinada fórmula P em um certo momento, isto já basta para
afirmar que se trata de uma fórmula válida. E, pelo contrário, se depois de
haver deduzido mil teoremas dos axiomas, P ainda não apareceu, não se pode
afirmar nada, porque P poderia aparecer após outros mil teoremas, permitindo-se
reconhecer sua validade, ou não aparecer nunca, por não ser válida. Mas não se
poderá afirmar em qual caso se está, mesmo depois das mil deduções .[Aga86].
A
decisão, dentro desse cálculo, seria possível possuindo-se um algoritmo capaz
de enumerar as expressões não válidas. A expressão P então aparecia dentro
desse conjunto de não válidas em algum momento. O teorema de Church de que se
está tratando consiste fundamentalmente na demonstração de que não existe
algoritmo capaz de enumerar as expressões não válidas, de maneira que fica
excluído a priori todo procedimento de decisão para as expressões do Cálculo de
Predicados, em geral. Para compreender as razões de semelhante fato seria
necessário valer-se das noções técnicas relacionados com os conceitos da
matemática recursiva, que excedem amplamente os limites deste trabalho.
Também
Church estava interessado no problema de Hilbert. O resultado a que Turing
tinha chegado em 1936, sobre o problema da decisão de Hilbert, havia sido
também alcançado por Church, alguns poucos meses antes, empregando o conceito
formalizado de lambda-definibilidade (ao invés do computável por uma Máquina de
Turing definido por Turing), no lugar do conceito informal procedimento efetivo
ou mecânico. Kleene, em 1936, mostrou que lambda-definibilidade é equivalente
ao conceito de recursividade de Gödel-Herbrand, e, nesse período, Church
formulou sua tese, estabelecendo que a recursividade é a própria formalização
do efetivamente computável. Isso foi estabelecido, no caso das funções dos
inteiros positivos, por Church e Kleene, em 1936. O cálculo-lambda, como
sistema elaborado por Church para ajudar a fundamentar a Matemática (1932/33) era inconsistente, como o
mostraram Kleene e Rosser (1935). Mas a parte do cálculo-lambda que tratava de
funções recursivas estava correta e teve sucesso. Usando sua teoria, Church
propôs uma formalização da noção de “efetivamente computável”, através do
conceito de lambda-definibilidade.
Turing, em 1936 e 1937, ao apresentar a sua noção de computabilidade associada
a uma máquina abstrata, mostrou que a noção Turing-computável é equivalente à
lambda-definibilidade [Hur80]. O
trabalho de Church e Turing liga fundamentalmente os computadores com as MT. Os
limites das MT, de acordo com a tese de Church-Turing, também descreve os
limites de todos os computadores.
O
processo que determina o valor de uma função através dos argumentos dessa
função é chamado de cálculo da função (ou computar uma função). Como foi
observado, a máquina de Turing pode ser matematicamente interpretada como um
algoritmo e, efetivamente, toda ação de uma máquina algorítmica como o
computador pode ser considerada como a de calcular o valor de uma função com
determinados argumentos. Este ‘insight’ é interessante, pois fornece uma
maneira de se medir a capacidade computacional de uma máquina. Necessita-se
somente identificar as funções que se é capaz de computar e usar esse conjunto
como medida. Uma máquina que compute mais funções que outra é mais poderosa.
A partir
dos resultados de Gödel, Turing e Church, pode-se dizer que existem funções para
as quais não existe uma seqüência de passos que determinem o seu valor, com
base nos seus argumentos. Dizendo-se de outra maneira, não existem algoritmos
para a solução de determinadas funções. São as chamadas funções não
computáveis. Isso significa que para tais funções não há nem haverá capacidade
computacional suficiente para resolvê-las. Logo, descobrir as fronteiras entre
funções computáveis e não computáveis é equivalente a descobrir os limites do
computador em geral. A tese de Church-Turing representa um importante passo
nesse sentido. A percepção de Turing foi a de que as funções computáveis por
uma MT eram as mesmas funções
computáveis acima referidas. Em outras palavras, ele conjeturou que o poder computacional
das MT abarcava qualquer processo algorítmico, ou, analogamente, o conceito da
MT propicia um contexto no qual todas as funções computáveis podem ser
descritas. Em síntese: as funções computáveis são as mesmas funções
Turing-computáveis. A importância disso está na possibilidade de se verificar o
alcance e limites de um computador. Na figura que segue pode-se visualizar como
se dá a ligação entre os mundos formal, matemático e computacional.
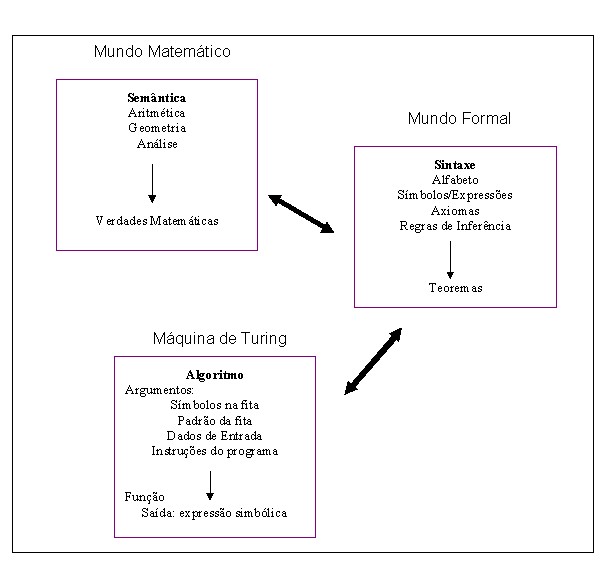
Figura: Relacionamento entre os mundos
formais, matemáticos e computacionais
(1) Em um
sistema axiomático parte-se de premissas aceitas como verdadeiras e regras
ditas válidas, que irão conduzir a sentenças verdadeiras. As conclusões podem
ser alcançadas manipulando-se símbolos de acordo com conjuntos de regras. A
Geometria de Euclides é um clássico exemplo de um procedimento tornado possível
por um sistema axiomático.
(2)
Parmênides (540 a 470 a.C.) negava a existência do movimento
("devir") e afirmava a existência de um único ser (panteísmo), tendo
enunciado o princípio da não contradição: 'algo não pode ser e não ser ao mesmo
tempo, sob o mesmo aspecto e no mesmo sujeito'. Seu discípulo Zenão (490 a 430
a.C.) foi o fundador da dialética e radicalizou a negação do movimento. Este
envolveria um paradoxo: para mudar completamente é preciso antes mudar
(3) Além do
mais interessa o estudo das obras do Filósofo pois tem um especial valor
pedagógico, ao apresentar de maneira unitária a maior parte dos problemas
lógicos, contemplados com o vigor característico que acompanha uma ciência
emergente, e mais acessível ao principiante que muitas apresentações modernas
de lógica formal
(4)
Modalidades são as expressões do tipo "é possível que...", "é
necessário que...".
(5) As definições
pretendem substancialmente explicitar os conceitos da geometria ("ponto é
aquilo que não tem partes"; "linha é comprimento sem largura",
etc.). Os postulados representam verdades indubitáveis típicas do saber
geométrico ("pode-se levar uma reta de qualquer ponto a qualquer
ponto"; "todos os ângulos retos são iguais"; etc.). Os axiomas
são verdades que valem universalmente, não só na geometria ("o todo é
maior que a parte"; "coisas que são iguais a uma mesma coisa são
iguais entre si", etc.).
(6) Neste
sentido foi o matemático grego que maior influência teve sobre a moderna teoria
dos números. Em particular Fermat foi levado ao seu 'último' teorema quando
procurou generalizar um problema que tinha lido na Arithmetica de Diophantus:
dividir um dado quadrado em dois quadrados (ver F.E. Robbins, P.Mich. 620:A
Series of Arithmetical Problems, Classical Philology, pg 321-329, EUA, 1929).
(7) Apenas
sob certo aspecto isto se justificaria. Em uma visão um tanto arbitrária e
simplista poderíamos dividir o desenvolvimento da álgebra em 3 estádios: (1)
primitivo, onde tudo é escrito em palavras; (2) intermediário, em que são
adotadas algumas simplificações; (3) simbólico ou final. Neste contexto,
Arithmetica deve ser colocada na segunda categoria.
(8) A
palavra algoritmo na matemática designa um procedimento geral de cálculo, que
se desenvolve, por assim dizer, automaticamente, poupando-nos esforço mental
durante o seu curso; este termo será depurado e aproveitado dentro da
Computação. Dele se tornará a falar mais à frente.
(9)
Lembrando algo que já foi dito, é importante ressaltar que desde suas origens
aristotélicas a lógica havia assumido claramente alguns recursos fundamentais,
como a estrutura formal, o emprego de certo grau de simbolismo, a
sistematização axiomática e o identificar-se com a tarefa de determinar as
"leis" do discurso (tomando, por exemplo, a linguagem como tema de
estudo), características que foram assumidas pela Lógica Moderna.
(10) Quando
aparecer uma controvérsia, já não haverá necessidade de uma disputa entre dois
filósofos mais do que a que há entre dois calculistas. Bastará, com efeito,
tomar a pena na mão, sentar-se à mesa (ad abacus) e (ao convite de um amigo,
caso se deseje), dizer um ao outro: Calculemos!" [Boc66].
(11) Newton
e Leibniz descobriram o princípio fundamental do cálculo de que uma integração
pode ser feita mais facilmente pela inversão do processo de diferenciação, no
cálculo das áreas[RA91].
(12) Em 1673
Gottfried Leibniz, usando uma engrenagem dentada, construiu uma calculadora
capaz de multiplicar, na qual um número era repetidamente e automaticamente
somado a um acumulador.
(13) A
Lógica Formal remonta particularmente a Aristóteles, como visto no capítulo dos
Primórdios, que a fundiu com a lógica filosófica em um conjunto de obras que
posteriormente chamou-se Organon. A lógica formal analisa detalhadamente as
diversas formas que podem adotar as operações lógicas, em particular o
raciocínio, com uma relativa independência dos seus conteúdos concretos.
(14) Leibniz
já tinha compreendido no século XVII que há alguma semelhança entre a disjunção
e conjunção de conceitos e a adição e multiplicação de números mas foi difícil
para ele formular precisamente em que consistia essa semelhança e como usá-la
depois como base para um cálculo lógico [Kne68].
(15) A base
do hardware sobre a qual são construídos todos os computadores digitais é formada
de dispositivos eletrônicos diminutos denominados portas lógicas. É um circuito
digital no qual somente dois valores lógicos estão presentes. Para se descrever
os circuitos que podem ser construídos pela combinação dessas portas lógicas é
necessária a álgebra booleana.
(16) Jevons
foi o primeiro a compreender que os métodos booleanos podem ser reduzidos às
regras do cálculo elementar, com a possibilidade, portanto, de ser mecanizados.
Em 1869 conseguiu construir uma máquina lógica apresentada no ano seguinte ao
público: era um dispositivo de 21 chaves para testar a validade de inferências
na lógica equacional. Algumas das características deste dispositivo foram
usadas mais tarde na implementação do computador. A máquina está conservada no
museu de História da Ciência em Oxford.
(17) O
emprego de quantificadores para ligar variáveis, principal característica do
simbolismo lógico moderno e que o torna superior em alguns aspectos à linguagem
vulgar e ao simbolismo algébrico de Boole, está entre as maiores invenções
intelectuais do século XIX [Kne68].
(18) Como já
se disse, idéia lançada por Leibniz de uma linguagem filosófica que seria um
simbolismo através do qual o homem estaria em condições de expressar seus pensamentos
com plena clareza e dirimir dúvidas através de simples cálculos.
(19) Sobre
número, dedução, inferência, proposições, premissas, etc.
(20) Quando a própria Lógica Formal reflete sobre seus
conteúdos.
(21) A lei
da tricotomia foi demonstrada no final do século XIX
(22) O
paradoxo de Russel, o paradoxo de Cantor, o paradoxo de Burati Forti, o
paradoxo de Richard, etc. Para exemplificar, vamos ao de Cantor, descoberto por
ele próprio em 1899: se S é o conjunto de todos os conjuntos, então seus subconjuntos
devem estar também entre os seus elementos. Conseqüentemente, o número cardinal
de S não pode ser menor do que o do conjunto dos subconjuntos de S. Mas isso,
pelo teorema do próprio Cantor, deveria ocorrer!
(23) Basta ler as palavras do matemático Sylvester em
sua controvérsia com Huxley. Dizia que a matemática se origina “diretamente das
forças e atividades inerentes da mente humana, e da introspecção continuamente
renovada daquele mundo interior do pensamento em que os fenômenos são tão
variados e exigem atenção tão grande quanto os do mundo físico exterior”. Para
ele, a matemática era “revelar as leis da inteligência humana”, assim como a
física revela as leis do mundo dos sentidos [Cos77].
(24) A lei comutativa da adição, por exemplo: para
quaisquer números a e b, a+b=b+a
(25) A tese logiscista compõe-se de duas partes: 1)Toda
idéia matemática pode ser definida por intermédio de conectivos lógicos (classe
ou conjunto, implicação, etc.); 2)Todo enunciado matematicamente verdadeiro
pode ser demonstrado a partir de princípios lógicos (“não contradição”,
“terceiro excluído”, etc.), mediante raciocínios puramente matemáticos.
(26) Para Brower, fundador desta escola – na verdade um
radicalizador das teses de Kronecker que não aceitava a teoria dos conjuntos –
o saber matemático escapa a toda e qualquer caracterização simbólica e se forma
em etapas sucessivas que não podem ser conhecidas de antemão: a atividade do
intelecto cria e dá forma a entes matemáticos, aproximando-se do apriorismo
temporal de Kant.
(27) Os logicistas tiveram de apelar a
princípios extra-lógicos – axioma de Zermelo, axioma do infinito – que ainda
hoje encontram-se sujeitos a calorosos debates e fortes reparos.
(28) Caminho
praticado por Hilbert no seu famoso trabalho Fundamentos da Geometria (1899), onde axiomatizou de modo rigoroso
a geometria euclidiana.
(29) No
início do século XX a matemática estava reduzida a três grandes sistemas
axiomáticos: aritmética, análise e conjunto, sendo a aritmética o mais
fundamental. Era natural que ele escolhesse esse sistema.
(30) John
von Neumann falava 5 línguas e foi um brilhante logicista,
matemático e físico. Além de lhe ser atribuída a invenção do primeiro
computador, ele estava no centro do grupo que criou o conceito de “programa
armazenado”, que potencializou extremamente o poder computacional das máquinas
que então surgiam.
(31) A simplicidade do problema de Hilbert é apenas
aparente, e somente após 70 anos de esforços foi encontrada a solução, por
Matijasevic, um matemático russo de apenas 22 anos na época. É uma solução
bastante complexa, dependendo tanto de resultados da Teoria do Números,
conhecidos há muitíssimos anos, como do trabalho anterior de três americanos,
Martin Davis, Julia Robinson e Hilary Putnan, que por sua vez baseia-se em
certos resultados fundamentais sobre lógica e algoritmos descobertos na década
de 30 por Kurt Gödel, Alan Turing, Emil Post, Alonso Church e Stephen Kleene. A
resposta a esse problema de Hilbert é: tal algoritmo não existe: o décimo
problema é indecidível.
(32) O termo finitístico é usado por vários
autores. Hilbert quis dizer que tal sistema deveria ser construído com um
número finito de axiomas e regras e todas prova dentro do sistema deveria ter
um número finito de passos.
(33) Quando
a notícia dos teoremas chegou aos Estados Unidos, o já então famoso John von
Neumann cancelou uma série de aulas que estava dando sobre o programa
hilbertiano e substituiu o resto do curso por um debate sobre o trabalho de Gödel
(34) As
conclusões de Gödel não significam que seja impossível construir uma prova
absoluta e finitista da aritmética. Significam que nenhuma prova deste tipo
pode ser construída dentro da aritmética., isto é, que esteja refletida a
partir de deduções formais da aritmética. Outras provas metamatemáticas da
consistência da aritmética foram construídas, em particular por Gerhard
Gentzen, da escola de Hilbert, em 1936, embora não finitistas e não
representáveis dentro do cálculo
aritmético, ou seja, estão fora das condições previstas por Hilbert.
(35) Os
resultados de Gödel tem conseqüências importantes também para a filosofia.
Sabe-se, graças a ele, ser impossível construir uma máquina que, de modo
consistente, resolva todos os problemas da matemática, com os recursos de um
sistema (certos problemas, por assim dizer, “não se deixam resolver” com os
recursos do sistema apenas). Mas de fato o matemático os resolve muitas vezes.
A conclusão a que se chega é que a mente humana é superior a uma máquina.
(36) Palavras
como procedimento efetivo e algoritmo representam conceitos básicos dentro da
Ciência da Computação. São noções que na época de Turing já eram utilizadas
pelos matemáticos, como por exemplo Frege e Hilbert (ver capítulos que tratam
dessas duas importantes figuras).
(37) Um ano mais tarde, trabalhando independentemente,
Alan Post publicou seu trabalho sobre uma máquina semelhante à de Turing.
(38) Uma Máquina de Turing Universal é uma Máquina de
Turing específica que lê na sua fita de alimentação, além de dados de entrada,
um programa R que é uma especificação de uma Máquina de Turing qualquer.
(39) Os
computadores possuem conjuntos de instruções que correspondem a regras fixas de
um sistema formal. Como provou Gödel, existem problemas não solucionáveis
dentro de um método axiomático e, portanto, há problemas que um computador não
resolve. Esta afirmação não deve ser vista como algo pessimista dentro da
Ciência da Computação: que um computador não possa resolver todos os problemas
não significa que não se possa construir uma máquina ou algoritmo específico
para solucionar determinado tipo de
problema [NN56].
(40)
Teoricamente é possível que a tese de Church seja derrubada em algum futuro,
caso surja um modelo alternativo de computação que seja publicamente aceitável
como algo que preenche totalmente as exigências de executar finitamente cada
passo e fazer operações não executadas por qualquer Máquina de Turing. Até a
data da confecção deste trabalho não surgiu ainda algo de consistente que
viesse a superar a tese de Church (o "computador quântico" - sobre o qual não há ainda uma literatura séria
disponível, para se poder falar algo dele nesse trabalho - é algo que poderia ocasionar um abalo nesse sentido)