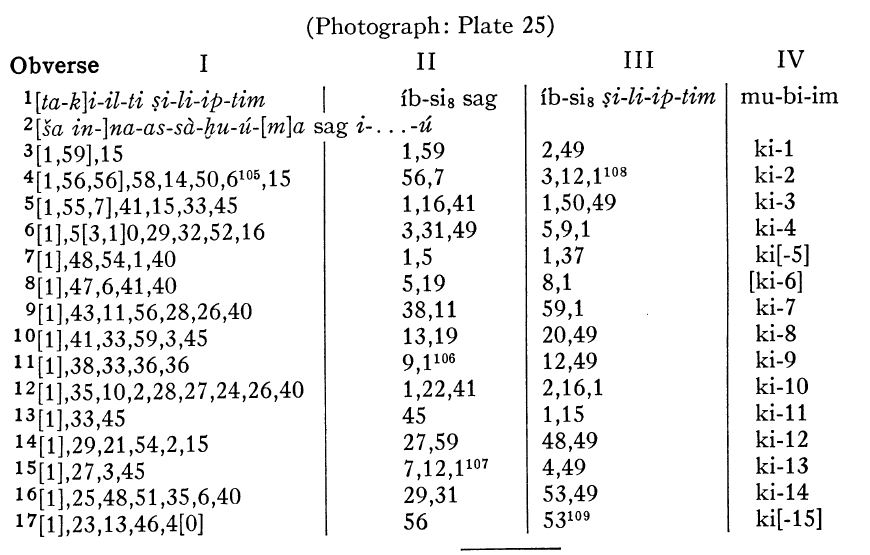
Duas formas de apresentação da matemática

Vemos que a matemática antiga sofreu um processo de lapidação priorizando o encadeamento do argumento. Este processo, ao mesmo tempo que posicionou a matemática como uma forma privilegiada de pensar, foi gradualmente omitindo características do espaço-tempo do problema original. Ainda mais, ao mesmo tempo em que foi lapidando-se no sentido de aparentar o desprendimento das coisas da vida, foi também confundindo-se com a sua própria apresentação. A forma dedutiva passou a significar a própria matemática, a despeito de outras possibilidades.

é a grande, interminável conversa das mulheres, parece coisa nenhuma, isto pensam os homens, nem eles imaginam que esta conversa é o que segura o mundo na sua órbita, não fosse falarem as mulheres umas com as outras, já os homens teriam perdido o sentido da casa e do planeta

(Saramago 1999, p 107)

Sendo “matemática” palavra de origem grega, “matemathike”, onde “máthema” significa compreensão, explicação, ciência, conhecimento, aprendizagem e “thike” significa arte ou técnica de acordo com o dicionário etimológico, houve quem argumentasse que matemática é essencialmente uma criação grega, uma confusão provocada pela etimologia do termo posteriormente adotado e um processo de criação cujo início coincide com a presença humana no mundo. No entanto, como verificou Arquimedes, a matemática dedutiva é uma forma de apresentação e portanto pressupõe um processo de criação de conceitos. A apresentação procedimental da matemática reflete esse processo de criação, aproximando a matemática do problema que se propõe a resolver. Em função desta aproximação com a vida, a apresentação procedimental foi sendo gradualmente subjugada como uma prática primitiva, uma matemática não evoluída, desvalorizada. Este panorama complexo atendeu a uma certa configuração de poder que se instituiu ao longo da antiguidade grega que valorizava o intelecto e a razão, como Platão explicita n’A República:

Sócrates — Enquanto os filósofos não forem reis nas cidades, ou aqueles que hoje denominamos reis e soberanos não forem verdadeira e seriamente filósofos, enquanto o poder político e a filosofia não convergirem num mesmo indivíduo, enquanto os muitos caracteres que atualmente perseguem um ou outro destes objetivos de modo exclusivo não forem impedidos de agir assim, não terão fim, meu caro Glauco, os males das cidades, nem, conforme julgo, os do gênero humano, e jamais a cidade que nós descrevemos será edificada. Eis o que eu hesitava há muito em dizer, prevendo quanto estas palavras chocariam o senso comum. De fato, é difícil conceber que não haja felicidade possível de outra maneira, para o Estado e para os cidadãos. (Platão, 1997, p.180-181)

Parte do texto A República que foi encontrado no lixão de Oxirrinco. Está catalogado como P.Oxy.LII 3679 Plato, Republic 5. 472e -473d. Fazendo a correspondência dos textos a partir das traduções da página de Oxirrinco e de Heinemann, (Plato 1969), parece que o fragmento mostrado nesta figura corresponde á parte transcrita ao lado.

A música do processo artesanal de confecção de uma rede, efetuado por Régis, na Fazenda Tamboril, povoado de Caraíbas, Pernambuco (Fonte: Projeto Tear: trabalho, educação, artes, redes, montagem produzida com os softwares screencastfy e cleapchamp create).

Deleuze e Guattari (2012) explicaram que a Ciência de Estado é o tecido, que se alonga longitudinalmente, mas é limitado nas laterais pela largura do tear. É um espaço estriado, demarcado pelo cruzamento de linhas verticais e horizontais, que dizem o como proceder. A Ciência de Estado é o tecido, limitado em largura e demarcado pelo cruzamento de regras. (Cafezeiro et al,2016).

O processo de conformação dos saberes é invariavelmente um atendimento a uma determinada conjuntura. Isto aplica-se não somente à matemática, mas a qualquer campo do conhecimento e configura duas ciências, uma legitimada (de Estado) e outra marginal (nômade):
	[E]ssa ciência nômade não pode ser “barrada”, inibida ou proibida pelas exigências e condições da ciência de Estado. (...) É que as duas ciências diferem pelo modo de formalização, e a ciência de Estado não para de impor sua forma de soberania às invenções da ciência nômade; só retém da ciência nômade aquilo de que pode apropriar-se, e do resto faz um conjunto de receitas estritamente limitadas, sem estatuto verdadeiramente científico, ou simplesmente o reprime e o proíbe. É como se o “cientista” da ciência nômade fosse apanhado entre dois fogos, o da máquina de guerra, que o alimenta e o inspira, e o do Estado, que lhe impõe uma ordem das razões. (Deleuze & Guattari 2012 p. 27-28)

A Ciência de Estado está sempre acompanhada da ciência nômade. Ainda mais, nenhuma delas se sustenta sozinha. Foi o que percebeu Arquimedes no campo da matemática ao pedir a Erastóstenes a demonstração de seus resultados. Deleuze & Guattari (2012 p. 228), mencionando o espaço liso como lugar da ciência nômade, advertiram: “Jamais acreditar que um espaço liso basta para nos salvar”.

Na tradição brasileira o tecido em fuxicos cresce acompanhando a conversa das mulheres, ciência também nômade, sem padrões fixados (Cafezeiro et al,2016). Na figura, fuxicos e artefatos para sua preparação. Os fuxicos serão costurados para formar colchas, toalhas ...

A ciência nômade é o feltro (Deleuze & Guattari 2012 p. 27-28), um emeranhado de fios. Não há um padrão uniforme em sua composição. Os fios se embolam numa desordem tal, como um antitecido, que não é homogêneo, mas é liso, ilimitado, não tem avesso. Assim, desregrada, se desenrola a ciência nômade, feita em fuxicos, poderia ser em qualquer direção, é na direção que acompanha a vida.

Um pedaço de sobra de pano,
um plano, um plano que se torce sobre si
ganhando, além de uma nova dimensão, uma outra topologia, não orientável,
que identifica o interior ao exterior e vice-versa,
como fazemos nós, humanos e fuxiqueiros,
com nossos universos dentro de nossas cabeças.
O leva e traz que se redobra e franze e
que mostra as suas dobras que plano, esconderia,
torna e retorna, como vento levado,
em espirais distraídas nas voltas que sempre em roda se constituirão.
O fuxico é uma tentativa que se realiza em suas possibilidades,
é a humanidade
que se descreve na construção matemática de um espaço projetivo,
com suas 4 dimensões sonhadas e seus infinitos continuamente humanos.

Um dos fundadores da Ciência da Computação Donald Knuth, ainda em tempos de afirmação da computação como uma ciência, percebeu que “[u]ma das maneiras de ajudar a tornar a ciência da computação respeitável é mostrar que ela está profundamente enraizada na história, não apenas em um fenômeno de curta duração” (Knuth, 1972, p.671). Com essa justificativa ele se dispôs a estudar a matemática babilônica para perceber semelhanças com a matemática algorítmica da computação. Knuth concluiu:

title=

Tabela de configuração da máquina de turing, (TURING 1936 p.233) o dispositivo teórico concebido por Alan Turing em 1936, que mais tarde tomaria materialidade como um computador.
Transcrição da tabela babilônica do período entre 1900 e 1600 a.C, para o cálculo do que viríamos a chamar "triângulos pitagóricos". É identificada como Plimpton 322 (NEUGEBAUER e SACHS 1945 cap III p.38-39).
Foto da tabela babilônica cuja transcrição é mostrada acima (Fonte:Columbia University Collections)

Os povos babilônicos e egípcios praticavam e expressavam sua matemática em uma forma algoritmica (sequência de passos, como uma receita de bolo). Esta forma de expressão matemática veio acompanhando a história do conhecimento humano, embora, nas reconstruções históricas produzidas pela da Ciência Moderna, ela só apareça em episódios pontuais, apontada como uma forma primitiva, não evoluída, da matemática. Entretanto, no século XX, esta forma de expressão matemática ganha evidência através dos computadores.

A Ciência da Computação se estabelece sobre o mesmo tipo de expressão matemática de três milênios antes da nossa era, e no entanto, representa para nós o supra-sumo da modernidade: os computadores, a robótica, a inteligência artificial.
Já não se pode dizer que a matemática algorítmica é primitiva.

		Os matemáticos babilônicos não se limitaram simplesmente aos processos de adição, subtração, multiplicação e divisão; eles eram peritos em resolver muitos tipos de equações algébricas. Mas eles não tinham uma notação algébrica tão transparente quanto a nossa; eles representavam cada fórmula por uma lista passo-a-passo de regras para sua avaliação, ou seja, por um algoritmo para calcular essa fórmula. Com efeito, eles trabalharam com uma representação de "linguagem de máquina" de fórmulas, em vez de uma linguagem simbólica. (Knuth, 1972, p.671)
	Knuth toma a matemática ocidental do século XX como referência. Fala das equações algébricas do nosso tempo como se elas pré-existissem aos problemas que se destinam a resolver. Assim, sua fala parece enaltecer a capacidade babilônica de resolver problemas, mas está subjulgando a matemática babilônica como um saber não tão evoluído quanto a matemática do nosso tempo.
	Ainda assim, a segunda metade do século XX aponta possibilidades efetivas de mudança nesta cena matemática, quando o uso disseminado dos computadores trouxer à luz novamente a maneira algorítmica, o “como fazer”. Aí então, aumentam as possibilidades de valorização de uma abordagem “problemática”, não “teoremática”, conforme a denominação de Deleuze & Guattari (2012 p. 26), onde “não se vai de um gênero a suas espécies por diferenças específicas, nem de uma essência estável às propriedades que dela decorram por dedução, mas de um problema aos acidentes que o condicionam e o resolvem (…) um ‘acontecimento’, muito mais do que uma essência.” .

	Referências
	CAFEZEIRO, Isabel; GADELHA, Carmem; ROCHA, André Campos; KUBRUSLY, Ricardo. Arremates em pesponto. Alinhavos sobre matemática e matemáticos. XII Encontro Nacional de Educação Matemática, 2016, São Paulo. Disponível aqui.
	DELEUZE, Gilles & GUATARRI, Felix. Mil Platôs. Capitalismo e Esquisofrenia, v. 5. São Paulo: Editora 34, 2012.
	KNUTH, D. Ancient Babilonian Algorithm. Communications of the ACM, v.15, n.7, 1972.
	NEUGEBAUER, O., SACHS, A. Mathematical Cuneiform Texts. American Oriental Society, New Haven, Conn., 1945.
	PLATÃO, A República. Corvisieri, E. (trad.) São Paulo: Editora Nova Cultural Ltda, 1997. Disponível aqui.
	PLATO, Plato in Twelve Volumes, Vols. 5 & 6 translated by Paul Shorey. Cambridge, MA, Harvard University Press; London, William Heinemann Ltd. 1969. Disponível pela Perseus Digital Library.
	SARAMAGO, J. Memorial do Convento. Bertrand Brasil, Rio de Janeiro, 1999.
	TURING, Alan. “On computable numbers, with an application to the Entscheidungs problem”. Proceedings of the London Mathematical Society, Series 2, n. 42, p. 230-265, 1936.

Programa de Pós-Graduação em
História das Ciências e das Técnicas e Epistemologia
UFRJ

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Duas formas de apresentação da matemática

um ‘acontecimento’, muito mais do que uma essência.”

Referências