|
|
Vértices |
Linhas |
Modelagem Geométrica e Sweeping
texto de: Éldman de Oliveira Nunes
1. Introdução
A modelagem geométrica consiste de um conjunto de métodos que visam descrever a forma e as características geométricas de um objeto. Ela provê uma descrição ou modelo muito mais analítico, matemático e abstrato que o real. Cria-se um modelo porque ele é mais conveniente e econômico que o objeto ou o processo real. Através desse modelo fica mais fácil e prático analisá-lo e testá-lo, como por exemplo a aerodinâmica de automóveis e aviões. Esta modelagem é o ingrediente básico de sistemas CAD/CAM, computadores gráficos, arte por computador, visão por computador, simulação, robótica e animação. Avanços em quaisquer destes campos dependem de quão bem definidos estão os modelos geométricos criados.
Métodos de modelagem geométrica são uma síntese de técnicas de muitas áreas como cálculo vetorial, geometria analítica e descritiva, teoria de conjuntos, análise numérica e matemática matricial, entre outras. Esta combinação de ferramentas matemáticas com a complexidade dos modelos geométricos requer grande esforço computacional.
2. Modelagem de Sólidos
Modelagem geométrica abrange outra área muitas vezes chamada de geometria computacional e estende-se além dessa para o campo da modelagem de sólidos, criando uma interessante união da geometria com a computação.
O termo modelagem de sólidos envolve um conjunto de teorias, técnicas e sistemas que enfocam a representação de sólidos informacionalmente completa, representação essa que permite (ao menos em princípio) que qualquer propriedade bem definida de qualquer sólido seja calculada automaticamente.
A metodologia de modelagem de sólidos é fundamental para diversas aplicações em engenharia. Ela requer o conceito de distinção entre dentro e fora de uma representação 3D de um determinado objeto, para que se possa obter o seu volume e as suas propriedades de massa.
Hoje, com a evolução desses métodos, podemos citar inúmeras outras aplicações, como simular mecanismos físicos, verificar a interferência em montagens mecânicas, fazer análises de elementos-finitos, simular e controlar a fabricação em máquinas de comando numérico através do sistema CAD/CAM e muitas outras.
Assim como um conjunto de linhas e curvas 2D não necessariamente descreve os limites de uma área fechada, uma coleção de planos e superfícies 3D não necessariamente forma um volume fechado. Em muitas aplicações, no entanto, é importante distinguir entre o lado de dentro, o de fora ou a superfície de um objeto 3D, e ser capaz de computar propriedades do objeto que dependem desta distinção. Em CAD/CAM, por exemplo, se um objeto sólido puder ser modelado de uma maneira que capture adequadamente sua geometria, então uma variedade de operações úteis pode ser executada antes do objeto ser fabricado. Podemos determinar se dois objetos interferem um com o outro; por exemplo, se um braço robô vai bater em objetos no seu ambiente, ou se uma ferramenta de corte irá cortar somente o material que se pretende remover. Na simulação de mecanismos físicos, como engrenagens, pode ser importante computar propriedades como volume e centro de massa. Além disso, algumas técnicas de Computação Gráfica, como a modelagem de transparência com refração, precisam ser capazes de determinar onde um feixe de luz entra e sai de um objeto sólido. Todas essas aplicações são exemplos de modelagem de sólidos. A necessidade de modelar objetos como sólidos resultou no desenvolvimento de várias maneiras especializadas de representá-los.
3. Representando Sólidos
A capacidade de uma representação em codificar coisas que têm a aparência de sólidos não determina, por si só, que esta representação é adequada para representar sólidos. Considere a representação de objetos como conjuntos de linhas retas, curvas, polígonos e superfícies. As linhas da Figura 1 formam um cubo sólido? Se assumirmos que cada conjunto de quatro linhas em cada lado do objeto limita uma face quadrada, então a figura é um cubo.
|
|
Vértices |
Linhas |
Figura 1. Um cubo em wireframe composto de 12 linhas retas
No entanto, não há nada na representação dada que exija que as linhas tenham que ser interpretadas assim. Por exemplo, a mesma representação poderia ser usada para desenhar a figura se alguma face (ou todas) estiver faltando. Como veremos adiante, algumas restrições extras são necessárias se quisermos ter certeza que uma representação deste tipo modele apenas sólidos. A seguinte lista de propriedades são desejáveis em um esquema de representação de sólidos: O domínio da representação deve ser grande o suficiente para permitir que um conjunto útil de objetos físicos seja representado. A representação deve ser não-ambígua, ou seja, não deve haver dúvida sobre o que está sendo representado, e uma dada representação deve corresponder a um e somente um sólido, ao contrário do que ocorre na Figura 1. Uma representação não-ambígua também é dita completa. Uma representação é única se puder ser usada para codificar qualquer sólido somente de uma maneira. Se uma representação pode assegurar a unicidade, então operações de comparação - como testar a igualdade de dois objetos - são fáceis. Uma representação precisa permite que um objeto seja representado sem aproximações. Assim como os sistemas gráficos que somente desenham linhas retas nos forçam a criar aproximações de curvas suaves, algumas representações de modelos de sólidos representam muitos objetos como aproximações. Quanto à validação, um esquema de representação deve tornar impossível a criação de representações inválidas (isto é, que não representam sólidos). Por outro lado, deve ser fácil criar uma representação válida, tipicamente com o auxílio de um sistema interativo de modelagem de sólidos. Gostaríamos também que os objetos mantivessem o fechamento após rotação, translação e outras operações. Isto significa que a execução de tais operações em sólidos válidos pode gerar apenas sólidos válidos. Uma representação deve ser compacta para economizar espaço, que pode por sua vez economizar tempo de transmissão em um sistema distribuído. Finalmente, uma representação deve permitir o uso de algoritmos eficientes para computar as propriedades físicas desejadas e - o mais importante para nós - para criar as imagens.
4. Esquemas de Representação de Sólidos Rígidos
A modelagem de sólidos é um importante aspecto da modelagem geométrica que é usada para criar e comunicar informações sobre sua forma. Ela envolve a criação e manutenção do modelo sólido para futuro acesso e análise.
Os primeiros sistemas de projeto assistido por computador (CAD) representavam desenhos (entidades bidimensionais) ao invés de sólidos tridimensionais. Em tais sistemas, além de usar esquemas ambíguos, as mudanças feitas em uma vista do objeto não se propagavam automaticamente para as outras vistas porque o sistema não sabia que as várias vistas eram projeções do mesmo objeto.
As representações de sólidos foram classificadas em ambíguas e não-ambíguas. As representações não-ambíguas são caracterizadas por serem completas e na sua maioria também por serem únicas. Os métodos de representação de sólidos denominam também as técnicas de modelagem de sólidos, que são as seguintes:
5. Modelagem por Varredura
(Sweep)A representação por varredura cria objetos baseada na noção de que uma curva C1 quando deslocada no espaço ao longo de uma trajetória dada por uma outra curva C2 descreve uma superfície que pode ser usada para definir um sólido. À curva C1 dá-se o nome de CONTORNO ou GERATRIZ e à C2, o nome de CAMINHO OU DIRETRIZ.
5.1 Varredura Translacional (Extrusão)
Um objeto "O" definido por varredura translacional é obtido pela translação de uma curva C ao longo de um vetor V, por uma distância D. A figura 2 exemplifica a criação de objetos por esta técnica. A varredura translacional de um retângulo gera um paralelepípedo, de uma circunferência gera um cilindro.
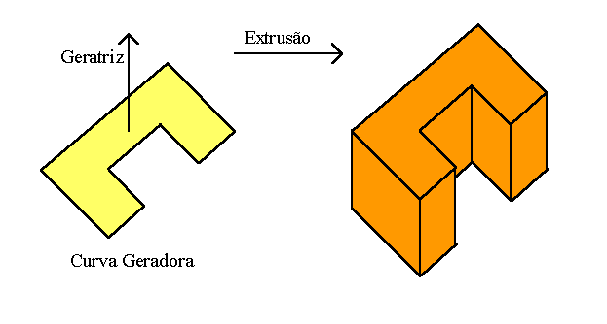
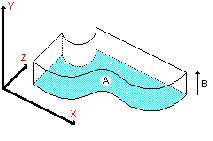
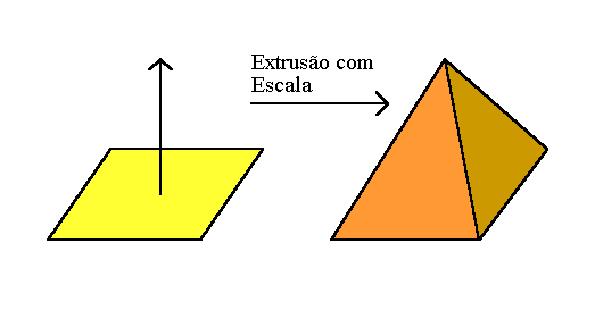
Figura 2 - Criação de objetos por varredura translacional
5.2 Varredura Rotacional
Neste tipo de modelagem por varredura a superfície do objeto é descrita por uma curva que gira em torno de um eixo. Na figura 6 temos, à esquerda, uma curva C e à direita o objeto gerado pela rotação de C em torno do eixo Y.
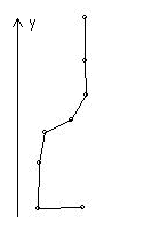


Figura 3 - Criação de objeto por varredura rotacional
6. Conclusão
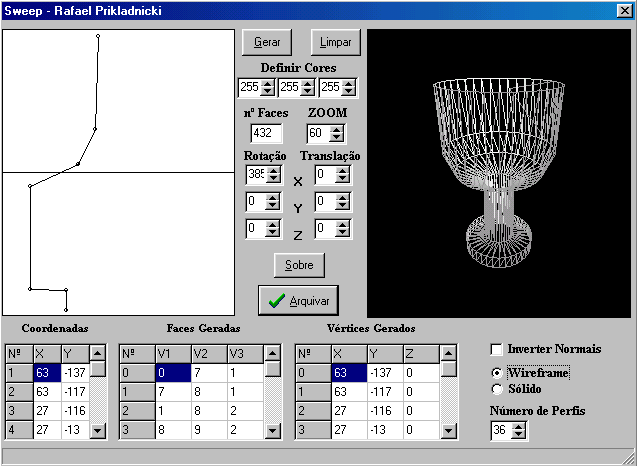
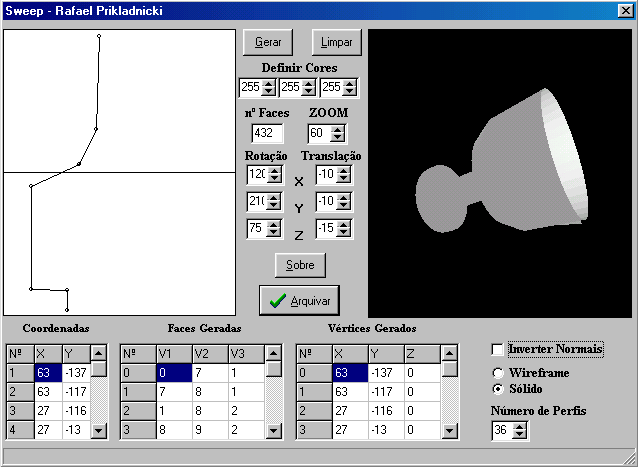
Demonstração de um programa exemplo de Sweep rotacional.
REFERÊNCIA BIBLIOGRÁFICA
J. D. Foley, A. van Dam, S.K.Feiner, J.F.Hughes. Computer Graphics  Principles and Practice.
Jonas Gomes, Luiz Velho. Computação Gráfica, Volume 1.
http://www.inf.unisinos.br/~osorio/CG-Doc/CG-Web/cg.html
http://jambo.caa.uff.br/~aconci/model.htm
http://www.inf.pucrs.br/~pinho/CG/Aulas/Modelagem/Modelagem3D.htm